Question

A solid sphere of radius $ R $ is charged uniformly. The electrostatic potential $ V $ is plotted as a function of distance $ r $ from the centre of the sphere. Which of the given below represents the best $ V $ vs $ r $ curve?
(A)

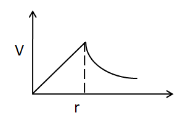
(B)

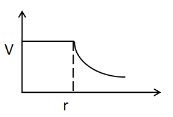
(C)

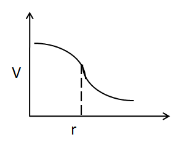
(D)

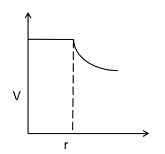
Answer 1

Hint: To solve this question, we need to use the relation between the electrostatic potential and the electric field. Then, we have to use the expressions for the electric field inside and outside a sphere and calculate the electrostatic potential in the regions inside and outside the sphere, from that relation.

Formula used: The formulae which are used to solve this question are given by
 $\Rightarrow E = - \dfrac{{dV}}{{dr}} $, here $ E $ is the electric field, $ V $ is the electrostatic potential, and $ r $ is the distance.
 $\Rightarrow {E_i} = \dfrac{{KQr}}{{{R^3}}} $, here $ {E_i} $ is the electric field inside a sphere of radius $ R $ and carrying a charge of $ Q $, at a distance of $ r $ from its centre.
 $\Rightarrow {E_0} = \dfrac{{KQ}}{{{r^2}}} $, here $ {E_0} $ is the electric field outside a sphere of radius $ R $ and carrying a charge of $ Q $, at a distance of $ r $ from its centre.

Complete step by step answer
We know that the electric field is related to the electrostatic potential by the relation
 $\Rightarrow E = - \dfrac{{dV}}{{dr}} $
So the potential becomes
 $\Rightarrow V = - \int\limits_\infty ^r {Edr} $...........................(1) (Potential at a point is always defined with respect to infinity)
Let the charge on the given solid sphere be $ Q $.
We know that the electric field outside the sphere at a distance of $ r $ from its centre is given by
 $\Rightarrow {E_0} = \dfrac{{KQ}}{{{r^2}}} $
So from (1) the potential outside the solid sphere becomes
 $\Rightarrow {V_0} = - \int\limits_\infty ^r {\dfrac{{KQ}}{{{r^2}}}dr} $
 $ \Rightarrow {V_0} = - KQ\left[ {\dfrac{{ - 1}}{r}} \right]_\infty ^r $
On substituting the limits, we get
 $\Rightarrow {V_0} = \dfrac{{KQ}}{r} $...........................(2)
Substituting $ r = R $ in the above equation, we get the potential on the surface of the solid sphere as
 $\Rightarrow {V_S} = \dfrac{{KQ}}{R} $...........................(3)
Now, we also know that the electric field inside a solid sphere is given by
 $\Rightarrow {E_i} = \dfrac{{KQr}}{{{R^3}}} $
So from (1) the potential inside the solid sphere becomes
 $\Rightarrow {V_i} = - \int\limits_\infty ^r {\dfrac{{KQr}}{{{R^3}}}dr} $
We can break the path of integral as
 $\Rightarrow V - {V_S} = - \int\limits_R^r {\dfrac{{KQr}}{{{R^3}}}dr} $
 $ \Rightarrow {V_i} = {V_S} - \dfrac{{KQ}}{{{R^3}}}\left[ {\dfrac{{{r^2}}}{2}} \right]_R^r $
Substituting the limits we get
 $\Rightarrow {V_i} = {V_S} - \dfrac{{KQ}}{{{R^3}}}\left\{ {\left[ {\dfrac{{{r^2}}}{2}} \right] - \left[ {\dfrac{{{R^2}}}{2}} \right]} \right\} $
 $ \Rightarrow {V_i} = {V_S} + \dfrac{{KQ}}{{2R}} - \dfrac{{KQ{r^2}}}{{2{R^3}}} $
From (3)
 $\Rightarrow {V_i} = \dfrac{{KQ}}{R} + \dfrac{{KQ}}{{2R}} - \dfrac{{KQ{r^2}}}{{2{R^3}}} $
 $ \Rightarrow {V_i} = \dfrac{{3KQ}}{{2R}} - \dfrac{{KQ{r^2}}}{{2{R^3}}} $...........................(4)
So the $ V $ vs. $ r $ curve is

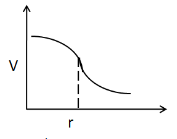
Hence, the correct answer is option C.

Note
The expressions of the electric fields at the inside and the outside regions of the solid spheres can be easily obtained by the application of the Gauss theorem. For this we just need to choose a spherical Gaussian surface at the desired location.