Question

A solid sphere of mass $2 \mathrm{~kg}$ is resting inside a cube as shown in Fig. The cube is moving with a velocity $\vec{v}=(5 t\hat{i}+2 t \hat{j}) m s^{-1} .$ Here tis the time in seconds. All surfaces are smooth. The sphere is at rest with respect to the cube. What is the total force exerted by the sphere on the cube?

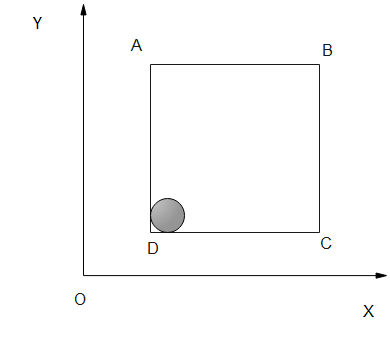
Answer 1

Hint: Normal Force of the body. Weight (also known as gravity force) is a pervasive force that acts at all times and must be counteracted in order to prevent a falling object. As the sphere is at rest there will be a normal force acting on a body and Also the force exerted by the cube. By the help of the block diagram we can calculate the all the forces acting on a sphere

Formula used:
$\mathrm{F}=\mathrm{m}\left[\mathrm{a}_{\mathrm{x}} \hat{\mathrm{i}}+\left(\mathrm{g}+\mathrm{a}_{\mathrm{y}}\right) \hat{\mathrm{j}}\right]$

Complete Step-by-Step solution:
The normal force is the force that a scale placed between the objects in contact would measure. According to the question Velocity of the cube is given Thus it will have acceleration and the mass of the cube is given.

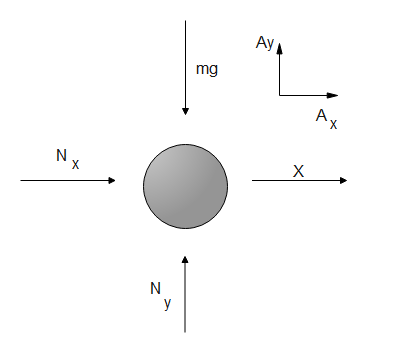
The velocity of the sphere is the same as that of the cube, which is given as:
$\vec{v}=5 t \hat{i}+2 t \hat{j}$.

Hence, acceleration of the sphere:
$\vec{a}=\dfrac{d \vec{v}}{d t}$
or $\vec{a}=(5 \hat{i}-2 \hat{j}) m s^{-2}$
$\Rightarrow \mathrm{F}=\mathrm{ma}$

$\Rightarrow \mathrm{F} = \mathrm{m}\left[\mathrm{a}_{\mathrm{x}}\hat{\mathrm{i}}+\left(\mathrm{g}+\mathrm{a}_{\mathrm{y}}\right)\hat{\mathrm{j}}\right]$

\[\Rightarrow\text{F }=\text{m}\sqrt{\left( \text{a}_{\text{x}}^{2}+{{\left( \text{g}+{{\text{a}}_{\text{y}}} \right)}^{2}} \right)}\]
$\Rightarrow\text{F }=2\times \sqrt{{{(5)}^{2}}+{{(10+2)}^{2}}}$
$\Rightarrow\text{F }=2\times \sqrt{25+144}~$
$\Rightarrow\text{F }=(2\times 13)N$

$\therefore \text{F }=26N$

The total force exerted by the sphere on the cube Is $26N$.

Note:
Relative acceleration is the comparison between the acceleration of two bodies or in the case of a rigid body, the acceleration of a point on the rigid body in relation to another point on that body. The net force must be zero - the weight balances the normal force. As in Newton's Third Law, it seems that weight and normal force are "equal and opposite forces" There will be both normal and tangential components of the relative acceleration term. Normal rigid body mechanisms are constructed in such a way that sliding takes place there.