Question

A solid consisting of a right circular cone of height 120 cm and radius 60 cm standing on a hemisphere of radius 60 cm is placed upright in a right circular cylinder full of water such that it touches the bottom. Find the volume of water left in the cylinder, if the radius of the cylinder is 60 cm and its height is 180 cm.

Answer 1

Hint: First, we will use the formula to calculate the volume of right circular cone is \[\dfrac{1}{3}\pi {r^2}h\], where \[r\] is the radius of the base and \[h\] is the height of the cone and then we will use the formula to calculate the volume of hemisphere is \[\dfrac{2}{3}\pi {r^3}\], where \[r\] is the radius of the hemisphere and then add the volumes to find the volume of the solid. Then we will subtract the volume of solid from the volume of the cylinder to find the volume of water left in the cylinder.

Complete step-by-step answer:
We are given the right circular cone of height \[h\] 120 cm and radius \[r\]60 cm.

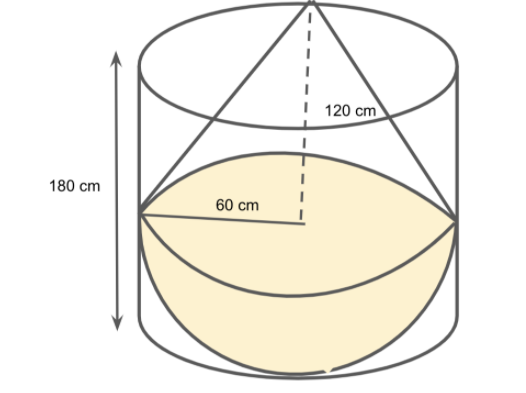
We know that the formula to calculate the volume of right circular cone is \[\dfrac{1}{3}\pi {r^2}h\], where \[r\] is the radius of the base and \[h\] is the height of the cone.

Substituting the value of \[\pi \], \[h\] and \[r\] in the above formula of the volume of the cone, we get
\[
   \Rightarrow {\text{Volume of cone}} = \dfrac{1}{3} \times \dfrac{{22}}{7} \times {\left( {60} \right)^2} \times 120 \\
   \Rightarrow {\text{Volume of cone}} = \dfrac{1}{3} \times \dfrac{{22}}{7} \times 3600 \times 120 \\
   \Rightarrow {\text{Volume of cone}} = \dfrac{{22}}{7} \times 3600 \times 40 \\
   \Rightarrow {\text{Volume of cone}} = \dfrac{{3168000}}{7}{\text{ c}}{{\text{m}}^3} \\
 \]

We know that the formula to calculate the volume of the hemisphere is \[\dfrac{2}{3}\pi {r^3}\], where \[r\] is the radius of the hemisphere.
Substituting the value of \[r\] and \[\pi \] in the above formula of the volume of the hemisphere, we get
\[
   \Rightarrow {\text{Volume of cone}} = \dfrac{2}{3} \times \dfrac{{22}}{7} \times {\left( {60} \right)^3} \\
   \Rightarrow {\text{Volume of cone}} = \dfrac{{22}}{7} \times 3600 \times 40 \\
   \Rightarrow {\text{Volume of cone}} = \dfrac{{3168000}}{7}{\text{ c}}{{\text{m}}^3} \\
 \]
Hence, we will now find the value of volume of solid by adding the volume of cone and volume of hemisphere, we get
\[
   \Rightarrow {\text{Volume of solid}} = \dfrac{{3168000}}{7} + \dfrac{{3168000}}{7} \\
   \Rightarrow {\text{Volume of solid}} = \dfrac{{3168000 + 3168000}}{7} \\
   \Rightarrow {\text{Volume of solid}} = \dfrac{{6336000}}{7}{\text{ c}}{{\text{m}}^3} \\
 \]
\[
   \Rightarrow {\text{Volume of cylinder}} = \dfrac{{22}}{7} \times {\left( {60} \right)^2} \times 180 \\
   \Rightarrow {\text{Volume of cone}} = \dfrac{{22}}{7} \times 3600 \times 180 \\
   \Rightarrow {\text{Volume of cone}} = \dfrac{{14256000}}{7}{\text{ c}}{{\text{m}}^3} \\
 \]

Now, subtracting the volume of solid from the volume of cylinder to find the volume of water left in cylinder, we get
\[
   \Rightarrow {\text{Volume of water left in cylinder}} = \dfrac{{14256000}}{7} - \dfrac{{6336000}}{7} \\
   \Rightarrow {\text{Volume of water left in cylinder}} = \dfrac{{14256000 - 6336000}}{7} \\
   \Rightarrow {\text{Volume of water left in cylinder}} = \dfrac{{7920000}}{7}{\text{ c}}{{\text{m}}^3} \\
   \Rightarrow {\text{Volume of water left in cylinder}} = 1131428.57{\text{ c}}{{\text{m}}^3} \\
 \]
Thus, the volume is \[1131428.57{\text{ c}}{{\text{m}}^3}\].

Note: In solving these types of questions, you should be familiar with the formula of volume of cone and volume of hemisphere. Some students use the formula of volume of sphere instead of the volume of the hemisphere, which is wrong. Then use the given conditions and values given in the question, and substitute the values in this formula, to find the required value.