Question

A solid consisting of a right circular cone of height 120cm and radius 60cm standing on a hemisphere of radius 60cm is placed upright in a right circular cylinder full of water such that it touches the bottom. Find the volume of water left in the cylinder, if the radius of the cylinder is 60cm and its height is 180cm.

Answer 1

Hint: From the given question, we need to find the volume of water in the cylinder. Therefore it can be calculated by removing the volume of solid from the volume of the cylinder. Volume of the solid is by $ \dfrac{2}{3}\pi {\left( r \right)^2}h + \dfrac{1}{3}\pi {\left( r \right)^3} $ and volume of cylinder is given by $ \pi {\left( r \right)^2}h $.

Complete step-by-step answer:
From the given question, we can say
Volume of water in the cylinder = Volume of cylinder - Volume of solid.
Given: A solid consisting of a right circular cone of height 120cm
The radius of the cone is 60cm.
Hemisphere is placed upright in a right circular cylinder full of water such that it touches the bottom.
Cone is standing on a hemisphere of radius 60 cm
Radius of the cylinder is 60 cm and its height is 180 cm.

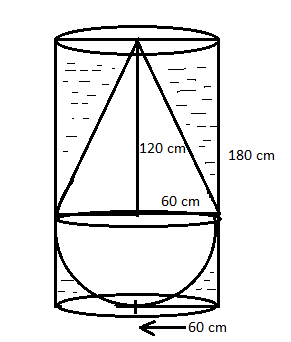
Radius of base of the cone $ {r_1} = 60cm $
Height of the cone $ {h_1} = 120cm $ that is two times of $ {r_1} $ .
Radius of the hemisphere $ {r_2} = 60cm = {r_1} $
Height of the cylinder $ {h_1} = 180cm $ that is three time of $ {r_1} $
Radius of the base of the cylinder\[{r_3} = 60cm = {r_1}\]
Now,
Volume of the solid $ = \dfrac{2}{3}\pi {\left( {{r_1}} \right)^3} + \dfrac{1}{3}\pi {\left( {{r_1}} \right)^2}\left( {2{r_1}} \right) $
 $ = \dfrac{2}{3}\pi {\left( {60} \right)^3} + \dfrac{1}{3}\pi {\left( {60} \right)^2}\left( {2 \times 60} \right) $
 $ = \dfrac{1}{3}\pi {\left( {60} \right)^3}\left[ {2 + 2} \right] $
 $ = \dfrac{4}{3}\pi {\left( {60} \right)^3} $
Again,
Volume of the cylinder $ = \pi {\left( {{r_1}} \right)^2}\left( {3{r_1}} \right) $
\[ = 3\pi {\left( {60} \right)^3}\]
Therefore,
Required volume of water left in the cylinder = Volume of cylinder - Volume of solid $ = \pi {\left( {60} \right)^3}\left[ {3 - \dfrac{4}{3}} \right] $
 $ = \dfrac{5}{3}\pi {\left( {60} \right)^3} $
=1130973.35 $ {\text{c}}{{\text{m}}^3} $
=1.131 $ {{\text{m}}^3} $ (approx.)
The volume of water left in the cylinder =1.131 $ {{\text{m}}^3} $

Note: The way we solved the problem is used in the same way to calculate the left out water after being filled by different shaped 3D figures. We need to calculate the volume of the figures and based on the requirements we can remove the volume of the figures immersed in water.