Question

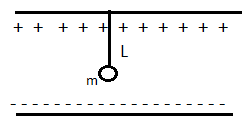
A small sphere carrying a charge $'q'$ is hanging in between two parallel plates by a string of length $l$. The time period of the pendulum is ${{T}_{o}}$. When parallel plates are charged, the time period changes to $10T$ . The ratio of $\dfrac{{{T}_{1}}}{{{T}_{2}}}$ is equal to ________

Answer 1

Hint: Find the effective acceleration due to gravity acting on the sphere due to the charged plates and then find the resultant time period to find the required ratio.

Complete step by step answer:
Given data is as follow
A small sphere carrying a charge $'q'$ is hanging in between two parallel plates by a string of length $l$. The time period of the pendulum is ${{T}_{o}}$ When parallel plates are charged, the time period changes to $10T$
We know that the time period of the sphere before charging the plates is
${{T}_{o}}=2\pi \sqrt{\dfrac{l}{g}}$

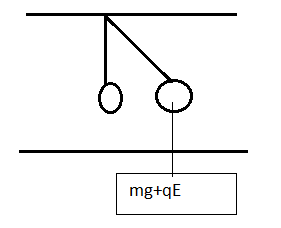
Let the mass of the sphere be
As shown in the above figure a sphere is having an additional weight that is $qe$ along with its own weight
Therefore the effective weight is as follows
$m{{g}^{'}}=mg+qe$
${{g}^{'}}=g+\dfrac{qe}{m}$
Now this $g$ effects or the final time period, the time period changes as follow
$T=2\pi \sqrt{\dfrac{l}{g'}}$
$\Rightarrow T=2\pi \sqrt{\dfrac{l}{g+\dfrac{qe}{m}}}$
Therefore the ratio of the time period before and after charging the plates is
$\dfrac{{{T}_{1}}}{{{T}_{2}}}=\dfrac{{{T}_{o}}}{10T}=\dfrac{2\pi \sqrt{\dfrac{l}{g}}}{2\pi \sqrt{\dfrac{l}{g+\dfrac{qe}{m}}}}$
$\Rightarrow \dfrac{{{T}_{o}}}{T}=10\sqrt{\dfrac{g+\dfrac{qe}{m}}{g}}$
Therefore the required ratio of the time periods is
$\dfrac{{{T}_{1}}}{{{T}_{2}}}=10\sqrt{\dfrac{g+\dfrac{qe}{m}}{g}}$

Note:
Due to the effect of the charge on the plates the weight of the sphere gets changed so the effective gravitational force changes which affects the time period of the pendulum.