Question

A single layered coil (solenoid) has a length $l$ and cross-sectional radius $R$ . The number of turns per unit length is equal to $n$. The magnetic induction at the centre of the coil where current $I$ flows through it is given by, $B = \dfrac{{x{\mu _0}nI}}{{\sqrt {1 + \left( {\dfrac{{2{R^2}}}{l}} \right)} }}$. Find $x$.

Answer 1

Hint: The general expression for the magnetic induction $B$ at the centre of a solenoid of length $l$ through which a current $I$ flows is given as, $B = \dfrac{{{\mu _0}nI}}{2}\left[ {\cos {\theta _1} - \cos {\theta _2}} \right]$ . The number of turns per unit length is equal to $n$ . The relation provided in the question is a simplified version of this general expression.

Complete step by step solution:
Step 1: Sketch a rough diagram representing the parameters of the solenoid and list the data given in the question.

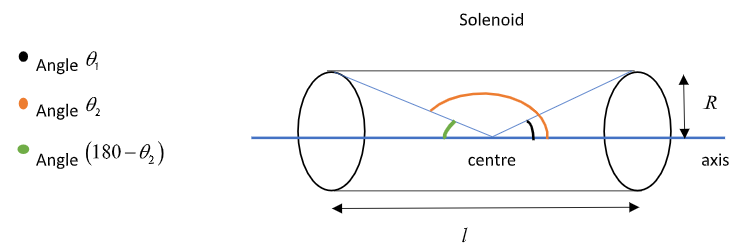
Given, the length of the solenoid is $l$ and its radius is $R$.
The number of turns per unit length is denoted by $n$.
The current $I$ flowing through the solenoid leads to a magnetic induction of $B = \dfrac{{x{\mu _0}nI}}{{\sqrt {1 + {{\left( {\dfrac{{2R}}{l}} \right)}^2}} }}$ at the centre of the coil.
Also, ${\mu _0}$ is the permeability of free space.
Step 2: Simplify the general expression for $B$.
Now we know that the magnetic induction at the centre of a solenoid is given by the equation, $B = \dfrac{{{\mu _0}nI}}{2}\left[ {\cos {\theta _1} - \cos {\theta _2}} \right]$ .
We know, $\cos \theta = \dfrac{{{\text{adjacent side}}}}{{{\text{hypotenuse}}}}$ , and from the figure the adjacent side is $\dfrac{l}{2}$ and hypotenuse is $\sqrt {{R^2} + {{\left( {\dfrac{l}{2}} \right)}^2}} $ .
Thus, $\cos {\theta _1} = \dfrac{{\left( {\dfrac{l}{2}} \right)}}{{\sqrt {{R^2} + {{\left( {\dfrac{l}{2}} \right)}^2}} }}$ .
We know, $\cos \left( {180 - {\theta _2}} \right) = - \cos {\theta _2}$ and from the figure, we have $\cos \left( {180 - {\theta _2}} \right) = \dfrac{{\left( {\dfrac{l}{2}} \right)}}{{\sqrt {{R^2} + {{\left( {\dfrac{l}{2}} \right)}^2}} }}$ or $\cos {\theta _2} = - \dfrac{{\left( {\dfrac{l}{2}} \right)}}{{\sqrt {{R^2} + {{\left( {\dfrac{l}{2}} \right)}^2}} }}$ .
Substituting for $\cos {\theta _1}$ and $\cos {\theta _2}$ in the equation for $B$ and simplifying we get,
$B = {\mu _0}nI\left( {\dfrac{{\left( {\dfrac{l}{2}} \right)}}{{\sqrt {{R^2} + {{\left( {\dfrac{l}{2}} \right)}^2}} }}} \right)$
Step 3: Equate the general equation and the equation for the magnetic induction given in the question to solve for $x$.
From the question, we have $B = \dfrac{{x{\mu _0}nI}}{{\sqrt {1 + {{\left( {\dfrac{{2R}}{l}} \right)}^2}} }}$ at the centre of the coil.
The general equation is $B = {\mu _0}nI\left( {\dfrac{{\left( {\dfrac{l}{2}} \right)}}{{\sqrt {{R^2} + {{\left( {\dfrac{l}{2}} \right)}^2}} }}} \right)$ .
Equating both equations, we get $\dfrac{{x{\mu _0}nI}}{{\sqrt {1 + {{\left( {\dfrac{{2R}}{l}} \right)}^2}} }} = {\mu _0}nI\left( {\dfrac{{\left( {\dfrac{l}{2}} \right)}}{{\sqrt {{R^2} + {{\left( {\dfrac{l}{2}} \right)}^2}} }}} \right)$ .
Cancel out the similar terms to get, $\dfrac{x}{{\sqrt {1 + {{\left( {\dfrac{{2R}}{l}} \right)}^2}} }} = \dfrac{{\left( {\dfrac{l}{2}} \right)}}{{\sqrt {{R^2} + {{\left( {\dfrac{l}{2}} \right)}^2}} }}$.
Rearranging to obtain, $x = \dfrac{{\left( {\dfrac{l}{2}} \right)\sqrt {1 + {{\left( {\dfrac{{2R}}{l}} \right)}^2}} }}{{\sqrt {{R^2} + {{\left( {\dfrac{l}{2}} \right)}^2}} }}$ .
Now, we take $\dfrac{4}{{{l^2}}}$ out of the square root, then $x = \dfrac{{\left( {\dfrac{l}{2}} \right) \times \left( {\dfrac{2}{l}} \right)\sqrt {\dfrac{{{l^2}}}{4} + {R^2}} }}{{\sqrt {{R^2} + \dfrac{{{l^2}}}{4}} }}$ .
We now can cancel similar terms to simplify the expression.

Therefore, $x = 1$ .

Additional information:
The solenoid is used to generate magnetic fields. This is done by allowing current to pass through it. The arrangement of two solenoids kept at some distance from each other and placed in an evacuated chamber can act as a magnetic bottle. The solenoids will act as a mirror or reflector to the approaching charged particles.

Note:
A change in the electric field induces a magnetic field. This concept is the working principle of the solenoid. Thus, whenever a magnetic field has to be generated in a body, the current is allowed to pass through it. Simplifications of the expressions must be done carefully.