Question

A short sighted person cannot see clearly beyond 2m calculate the power of the lens that is required to correct this vision and also give the type of lens.

Answer 1

Hint: As a first step, one could read the question well and hence note down the important points given also the quantities to be found. One could recall the lens formula and also the expression for power and then carry out the substitutions accordingly to find the answer.

Formula used:
Lens formula,
$\dfrac{1}{f}=\dfrac{1}{v}-\dfrac{1}{u}$
Power,
$P=\dfrac{1}{f}$

Complete step-by-step solution:
In the question, we are given the case of a person who is suffering from short sightedness. We are also told that this person cannot see beyond a distance of 2m. We are supposed to calculate the power of the lens that is used to correct this defect and also give the type of lens used for the same.
Since the farthest this person can see is 2m away, one should use a lens such that the image of the object at infinity is formed at this farthest point. That is,
$u=-\infty $
$v=-2m$
Recalling lens formula and then substituting these values,
$\dfrac{1}{f}=\dfrac{1}{v}-\dfrac{1}{u}$
$\Rightarrow \dfrac{1}{f}=\dfrac{1}{-2}+\dfrac{1}{\infty }$……………………………….. (1)
Now let us recall the expression for power of a lens.
$P=\dfrac{1}{f}$
Where, f is focal length in meters. Now, from (1) we have,
$\therefore P=-0.5D$
Therefore, we found the power of the lens to be -0.5D.
Also, since the person is suffering from myopia, the corrective lens used is a concave lens.

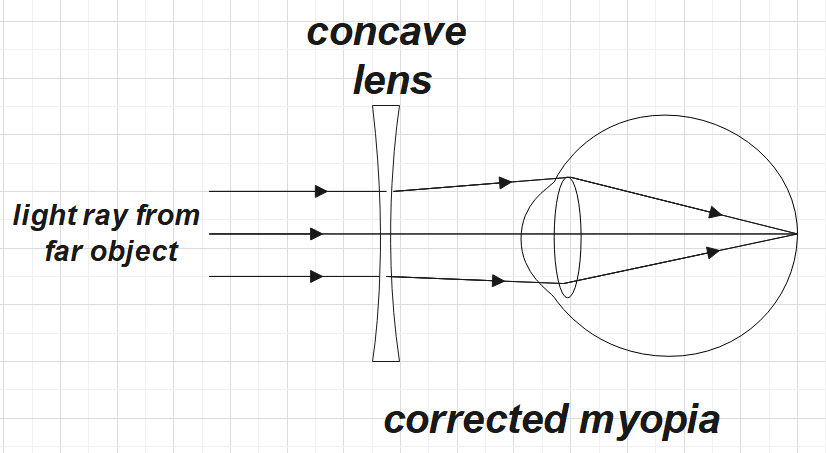
Note:Now another eye defect is the hypermetropia or the far sightedness. In this defect, the patient won't be able to see the nearby objects but only the far away objects. This defect can also be corrected using a convex lens of required power. Astigmatism, cataract are all other eye defects.