Question

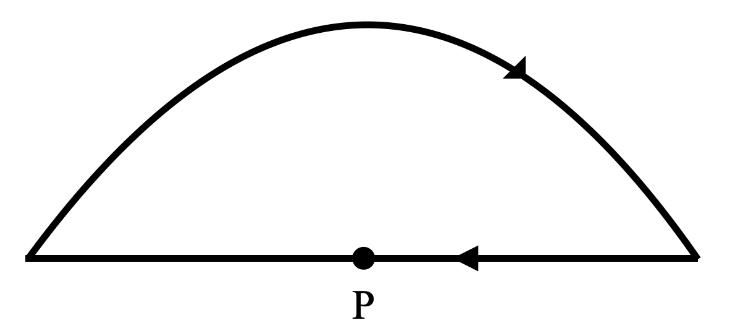
A semicircular arc of radius r and a straight wire along the diameter, both are carrying the same current i. Find out magnetic force per unit length on the small element P, which is at the centre of curvature?

A. $\left( \dfrac{{{\mu }_{0}}{{i}^{2}}}{4r} \right)$
B. $\left( \dfrac{{{\mu }_{0}}{{i}^{2}}}{2r} \right)$
C. $\left( \dfrac{{{\mu }_{0}}{{i}^{2}}}{r} \right)$
D. $\left( \dfrac{2{{\mu }_{0}}{{i}^{2}}}{r} \right)$

Answer 1

Hint: Biot-Savart’s law confirms that there won’t be any magnetic field at P due to the straight wire. Because, the point lies on the wire. We need to find the magnetic field at P due to the semicircular arc. We can find the force using the formula,
$F=Bil$

Where,
$B$ is the magnetic field at that location
$i$ is the current
$l$ is the length of the wire.

Formula Used:
Magnetic field due to the semicircular arc,
$B=\dfrac{{{\mu }_{0}}i}{4r}$

Where,
${{\mu }_{0}}$ is the permittivity of the material
$i$ is the current through the arc
$r$ is the radius of the arc

Force per unit length is,
$\dfrac{F}{l}=Bi$

Where,
$B$ is the magnetic field
$i$ is the current through the point

Complete step by step answer:
The radius of the semicircular arc is = r

Current passing through the loop = i

We can find the magnetic field due to a semicircular arc at the centre using Biot-Savart’s law. It is given by,
$B=\dfrac{{{\mu }_{0}}i}{4r}$

Where,
${{\mu }_{0}}$ is the permittivity of the material
$i$ is the current through the arc
$r$ is the radius of the arc

So, at point P the magnetic field is,
$B=\dfrac{{{\mu }_{0}}i}{4r}$

Now, the current flowing through wire at P is i

The force per unit length due to the Magnetic field on a wire is,
$\dfrac{F}{l}=Bi$...................(1)

Where,
$F$ is the force on the wire
$B$ is the magnetic field at that location
$i$ is the current going through the wire
$l$ is the length of the wire

So, in this case, the force per unit area will be given by,
$\dfrac{F}{l}=Bi$
$\Rightarrow \dfrac{F}{l}=(\dfrac{{{\mu }_{0}}i}{4r})i$
$\Rightarrow \dfrac{F}{l}=\dfrac{{{\mu }_{0}}{{i}^{2}}}{4r}$

So, the magnetic force per unit length is
$\dfrac{{{\mu }_{0}}{{i}^{2}}}{4r}$

Hence, the correct option is (A).

Note: You can divide the entire loop into different segments. Find the magnetic field due to each segment. Don’t consider the segments which are aligned with the point at which we are finding the magnetic field. After that we can use the simple equation (1) to find force per unit length.