Question

A satellite is launched in the equatorial plane in such a way that it can transmit signals upto $60 ^{\circ}$ latitude on the earth. Then the angular velocity of the satellite is:

A. $\dfrac{GM}{8R^3}$
B. $\dfrac{GM}{2R^3}$
C. $\dfrac{GM}{4R^3}$
D. $\sqrt{\dfrac{3\sqrt{3}GM}{8R^3}}$

Answer 1

Hint: The question is from the chapter ‘Gravitation’ and can be solved by using the formula of the time period of the satellite in an orbit. Angular velocity of a body is inversely related to its time period.
Formula used:
Formula for the time period of a revolving object:
 $T=2\pi \sqrt{\dfrac{r^{3}}{GM}}$
The angular velocity is related to time period as:
$\omega=\dfrac{2\pi}{T}$

Complete answer:
Given:
The range of the satellite: $60 ^{\circ}$ latitude of earth.
The orbital time period of a satellite orbiting in earth's orbit, at a height of r=R+h is given as:
$T=2\pi \sqrt{\dfrac{r^{3}}{GM}}$

The angular velocity is given as:
$\omega=\dfrac{2\pi}{T}$
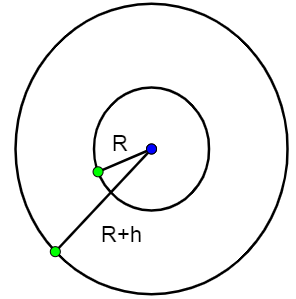
We require finding the height r of the satellite.
If we consider the fact that $60 ^{\circ}$ latitude of earth is nothing but $R\tan 60 ^{\circ}$. This is the range, with R being the radius of earth. The range satellite, for the point where it is at a height h above the equatorial plane :
Range= $\sqrt{(R+h)^{2}-h^2}$
Thus, in our case
$R\dfrac{1}{\sqrt{3}}=$$\sqrt{(R+h)^{2}-h^2}$
$\dfrac{R^2}{3}=2Rh+h^2$

By solving, this quadratic equation, we get:
$h=-R \pm \dfrac{2 R}{\sqrt{3}}$
Thus, using the formula for time period now,
r=R+h;
$r=\dfrac{2R}{\sqrt{3}}$
$T=2\pi \sqrt{\dfrac{(2 R / \sqrt{3})^{3}}{GM}}$

Thus the angular velocity is obtained as
$\omega=\dfrac{2 \pi}{2 \pi \sqrt{\dfrac{(2 R / \sqrt{3})^{3}}{GM}}}$
$\sqrt{\dfrac{3\sqrt{3}GM}{8R^3}}$

So, the correct answer is “Option D”.

Additional Information:
A satellite is a body that revolves around other bodies like planets. Geostationary satellites have their period of revolution the same as the rotation period of the earth. Thus, geostationary satellites appear at the same position in the sky.

Note:
The formula for T was derived using circular orbit approximation for the case of satellites. The centripetal force of the satellite in its circular motion is balanced by the gravitational force that earth exerts on it.