Question

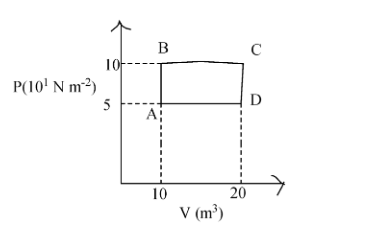
A sample of 2 kg of helium (assumed ideal) is taken through the process ABC and another sample of 2 kg of the same gas is taken through the process ADC. Then the temperature of the states A and Bare (given R= 8.3J/ mol K)

Answer 1

Hint: The gas is given at particular pressure and volume, the temperature is calculated by the ideal gas equation. The number of moles can be calculated with a given mass of the sample and molecular mass of the sample.

Complete step by step answer:
Let us understand the ideal gas equation.
The ideal gas equation is the equation that tells the effect of pressure and temperature on the volume of an ideal gas.
The ideal gas equation can be derived as:
According to Boyle's law, the volume of the gas is inversely proportional to the pressure.
\[V\propto \dfrac{1}{P}\]
According to Charles law, the volume is directly proportional to temperature.
\[V\propto T\]
According to Avogadro's law, the volume is directly proportional to the number of moles.
\[V\propto n\]
Combining all these, we get the ideal gas equation.
\[\begin{align}
  & V\propto \dfrac{1}{P}\text{x T x n} \\
 & \text{V = R x }\dfrac{1}{P}\text{ x T x n} \\
 & \text{PV=nRT} \\
\end{align}\]
R is the gas constant.
In the question, it is given 2 kg of helium and molecular mass of helium is 4, the number of moles can be calculated as,
\[n=\dfrac{\text{given mass (grams)}}{\text{molecular mass}}=\dfrac{2000}{4}=500\]
Now, at point A, the pressure is\[5\text{x}10N{{m}^{-2}}\] and volume is \[10{{m}^{3}}\] and the value of R= 8.3J/ mol K.
So, according to the ideal gas equation,
\[\begin{align}
  & {{\text{P}}_{A}}{{\text{V}}_{A}}\text{=nR}{{\text{T}}_{A}} \\
 & {{\text{T}}_{A}}=\dfrac{{{\text{P}}_{A}}{{\text{V}}_{A}}}{nR}=\dfrac{5\text{x}10\text{x}10}{500X8.3}=0.120K \\
\end{align}\]
Now at point B, the pressure is \[10\text{x}10N{{m}^{-2}}\] and volume is \[10{{m}^{3}}\] and the value of R= 8.3J/ mol K.
By applying the ideal gas equation, we get.
\[\begin{align}
  & {{\text{P}}_{B}}{{\text{V}}_{B}}\text{=nR}{{\text{T}}_{B}} \\
 & {{\text{T}}_{B}}=\dfrac{{{\text{P}}_{B}}{{\text{V}}_{B}}}{nR}=\dfrac{10\text{x}10\text{x}10}{500X8.3}=0.240K \\
\end{align}\]

Hence, the temperature at A is 0.120 K and at B is 0.240K.

Note: The given mass should always be converted into the number of moles. The ideal gas equation is only applicable to the ideal gas. The gas is ideal should be mentioned in the question. Real gases do not follow this equation.