Question

A roller coaster is designed such that riders experience “weightlessness” as they go round the top of a hill whose radius of curvature is 20m. The speed of the car at the top of hill is between -

Answer 1

Hint: The circular motion of the roller coaster in this case needs to be understood, to solve this problem. Making a free body diagram of the problem is required. Equating the forces acting on the roller coaster, will give the solution. Do remember, that weightlessness means that the normal force acting against the weight of the body will be zero.

Complete step by step answer:
Let’s start by making a free body diagram of the problem given to us.

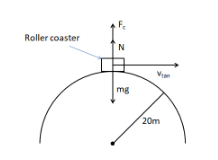
As per the problem, we have a hill having a radius of curvature of 20m. That is: r=20m. The riders will experience the weightlessness phase, when they pass through the top of the hill. As the roller coaster’s car passes through the top of the hill, it follows a circular motion. At the top of the hill, let’s consider the mass of the roller coaster’s car to be (m). The acceleration due to gravity (g) acting downwards acts on the rollercoaster. Hence, the weight of the roller coaster’s car: $\left( {{F}_{g}}=mg \right)$ acts downward from the centre of mass of the roller coaster’s car. Correspondingly a Normal force (N) acts vertically upward from the centre of the mass of the roller coaster’s car.

Due to the circular motion of the roller coaster’s car, centrifugal force acts on the roller coaster’s car. The centrifugal force pushes the body away from the centre. Hence, the centrifugal force acting on the body is given by: $\left( {{F}_{c}}=\dfrac{mv_{\tan }^{2}}{r} \right)$. The velocity of the roller coaster’s car is (v). Here, at the top of the hill, it is also the tangential velocity of the roller coaster’s car. Hence: $\left( v_{\tan }^{{}}=v \right)$.

Therefore, equating all the forces acting on the body, we get: ${{F}_{c}}+N={{F}_{g}}$. However, since the roller coaster experiences weightlessness, hence, the Normal force acting on the body is equal to zero. Therefore: ${{F}_{c}}={{F}_{g}}\Rightarrow \dfrac{m{{v}^{2}}}{r}=mg\Rightarrow \dfrac{{{v}^{2}}}{r}=g\Rightarrow {{v}^{2}}=gr\Rightarrow v=\sqrt{gr}$.
Substituting in the value of the radius of curvature (r=20m) and $\left( g\approx 10\ m{{s}^{-2}} \right)$, we get: $v=\sqrt{gr}\Rightarrow v=\sqrt{10.20}\Rightarrow v=\sqrt{200}\Rightarrow v\approx 14.14\ m{{s}^{-1}}$.
Hence, the correct answer is option C.

Note:
In an actual roller coaster, there are safety mechanisms in place to ensure the car stays in the roller coaster’s track instead of flying away whenever such curves are there, when the roller coaster’s car can experience weightlessness.
Quite a few times, when we are travelling in a lift coming down rapidly, we can also feel weightlessness. During this time, the body fluids seem to rise as there isn’t any gravity pushing them down.