Question

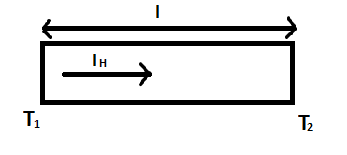
A rod of length l and cross sectional area A has a variable conductivity given by $K = \alpha T$ where $\alpha $ is a positive constant and T is temperature in kelvin. Two ends of the rod are maintained at temperature ${T_1}$ and ${T_2}$ $({T_1} > {T_2})$. Heat current flowing through the rod will be
A) $\dfrac{{A\alpha ({T_1}^2 - {T_2}^2)}}{l}$
B) $\dfrac{{A\alpha ({T_1}^2 + {T_2}^2)}}{l}$
C) $\dfrac{{A\alpha ({T_1}^2 + {T_2}^2)}}{{3l}}$
D) $\dfrac{{A\alpha ({T_1}^2 - {T_2}^2)}}{{21}}$

Answer 1

Hint: We can form an equation using the fact that rate of change of current with temperature is equal to product of conductivity and area upon length given as $\dfrac{{dI}}{{dT}} = \dfrac{{KA}}{l}$ and the integration of this discrete current will provide the heat current flowing through the rod.

Complete step by step answer:
Given conductivity (K) is equal to $\alpha T$. It is given that ${T_1} > {T_2}$ and heat current $\left( {{I_H}} \right)$ flows from higher to lower temperature, thus it’s direction is from ${T_1}$ to ${T_2}$.
In conduction, the change of current with respect to temperature is given as
$\dfrac{{KA}}{l}$.
$ \Rightarrow \dfrac{{dI}}{{dT}} = \dfrac{{KA}}{l}$

Solving this to get the value of heat current:
$dI = KA\dfrac{{dT}}{l}$
Substituting the given value of K:
$dI = \alpha TA\dfrac{{dT}}{l}$
Integration of this current will give the value of heat current $\left( {{I_H}} \right)$. So integrating both sides of the equation from ${T_1}$ to ${T_2}$, we get:
$
  \int {dI} = \int\limits_{{T_1}}^{{T_2}} {\alpha TA\dfrac{{dT}}{l}} \\
\implies {I_H} = \dfrac{{\alpha A}}{l}\int\limits_{{T_1}}^{{T_2}} {TdT} \\
\implies {I_H} = \dfrac{{\alpha A}}{l}{\left[ {\dfrac{{{T^2}}}{2}} \right]^{{T_2}}}_{{T_1}} \\
 $
Subtracting upper limit from lower limit after substitution:
${I_H} = \dfrac{{\alpha A}}{{2l}}\left( {{T_1}^2 - {T_2}^2} \right)$
Therefore, the heat current flowing through the rod will be $\dfrac{{\alpha A}}{{2l}}\left( {{T_1}^2 - {T_2}^2} \right)$.

So, the correct answer is “Option D”.

Note:
Conduction basically is a process of heat transfer between objects, where it gets transferred from the one at higher temperature to the one at lower.
We use differentiation to denote the rate of changes while we use integration for the summation of that discrete data.
Remember for integrating mathematically:
$\int {{x^n} = \dfrac{{{x^{n + 1}}}}{{n + 1}}} $ and when it has limits, always subtract the lower limit from the upper limit.