Question

A rod is hinged from one end. It is brought to a horizontal position and released. The angular velocity of the rod, when it is in vertical position is
\[\begin{align}
  & A.~~~~~~~~~~~~~~\sqrt{\dfrac{2g}{l}}~~~~~~ \\
 & B.~~~~~~~~~~~~~~\sqrt{\dfrac{3g}{l}}~~~~~ \\
 & C.~~~~~~~~~~~~~~\sqrt{\dfrac{g}{2l}}~~~~~ \\
 & D.~~~~~~~~~~~~~~\sqrt{\dfrac{g}{l}}~~~~~ \\
\end{align}\]

Answer 1

Hint: This problem can be easily solved by applying energy conservation from horizontal position to vertical position. Only conservative forces have done work during this entire path, so energy conservation can be applied. The entire kinetic energy gained by the rod is equal to the potential gravitational energy lost.

Complete Step By Step Solution:

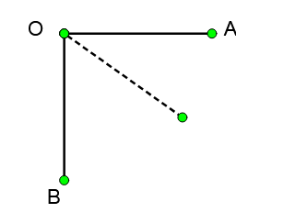
A rod is hinged at O and released from A under gravity it falls and reaches a position B. The forces acting on it during this journey are gravity and force from hinge only.
Force from hinge is non conservative but the work done by this force on rod is zero. This is because the point of application of this force i.e. the hinged part of rod does not move. So work is done only by gravity, which is a conservative force. Thus energy Conservation is applicable here.
Let us assume the mass of the rod to be ‘m’. Acceleration due to gravity is g and length of rod is l. Let's assume gravitational potential energy to be zero at OA.
The total potential energy at when rod is along OA is 0. The total Kinetic energy at OA is also 0, as the rod is just released and every point of the rod is at rest. Therefore the total mechanical energy of the rod at OA is 0.
When rod is along OB, total potential energy of rod is $\dfrac{-mgl}{2}$ , as the center of mass of rod (which is at exact) of rod is $\dfrac{l}{2}$ below line of reference. If a body is moving such that every point on it moves in circular orbit about a same point, then its kinetic energy can be written as $\dfrac{I{{w}^{2}}}{2}$ , where I is moment of inertia of body about the point and w is angular velocity of body about that point. Here hinged part of rod is that point so we can write kinetic energy of rod as $\dfrac{{{I}_{O}}{{w}^{2}}}{2}$ . Moment of inertia about O is$\dfrac{m{{l}^{2}}}{3}$. So total mechanical energy of rod at OB is
$\dfrac{-mgl}{2}+\dfrac{m{{l}^{2}}{{w}^{2}}}{6}$
By energy conservation,
$\dfrac{-mgl}{2}+\dfrac{m{{l}^{2}}{{w}^{2}}}{6}=0$
$\begin{align}
  & \dfrac{m{{l}^{2}}{{w}^{2}}}{6}=\dfrac{mgl}{2} \\
 & \\
\end{align}$
On solving we get,
$w=\sqrt{\dfrac{3g}{l}}$
So the correct option is B.

Note: This problem can also be solved using the work energy theorem, both of the methods are quite similar, only the key point is work done by friction is zero as explained above. But it is recommended to not solve it using kinematic approach as it will make the question unnecessarily lengthy because angular acceleration here is continuously changing due to changing t