Question

A road roller takes 750 revolutions to move once over to level a road. Find the area of the road if the diameter of a road roller is 84 cm and length is 1 m.

Answer 1

Hint: The diameter and length of the road roller are 84 cm and 1 meter. We know the relation between meters and centimeters, \[100cm=1m\] . Use this relation and convert the diameter into meters. The area covered by the road roller in one revolution is equal to its curved surface area. We know that the road roller is in the shape of a cylinder and the curved surface area of the road roller is given by the formula, \[2\pi \left( radius \right)\left( length\,of\,the\,cylinder \right)\] . Use this formula and get the area covered by the road roller in one revolution. Now, multiply by 750 in the curved surface area to get the area covered by the road roller in 750 revolutions. Solve it further and get the required area.

Complete step-by-step answer:

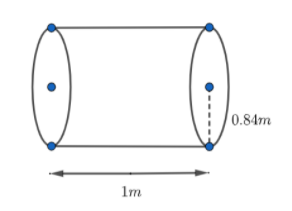
According to the question, it is given that,
The diameter of the road roller = 84 cm ……………………………………..(1)
The length of the road roller = 1 meter ………………………………………(2)
We know the relation between meters and centimeters, \[100cm=1m\] ………………………………...(3)
Now, from equation (1) and equation (3), we get
The diameter of the road roller = 84 cm = \[0.84\times 100cm=0.84m\]
We know that radius is half of the diameter.
Now, on dividing the diameter by 2, we get
The diameter of the road roller = \[\dfrac{0.84}{2}=0.42\] ……………………………………..(4)
The area covered by the road roller in one revolution is equal to its curved surface area.
We know that the road roller is in the shape of a cylinder and the curved surface area of the road roller is given by the formula, \[2\pi \left( radius \right)\left( length\,of\,the\,cylinder \right)\] …………………………………………(5)
Now, from equation (2), equation (4), and equation (5), we get
The curved surface area of the road roller = \[2\pi \left( 0.42m \right)1m=\left( 0.84\pi \right){{m}^{2}}\] ………………………………………(6)
It is also given that the road roller is making 750 revolutions.
Since in one revolution, the road roller covers an area of \[\left( 0.84\pi \right){{m}^{2}}\] so, in 750 revolutions the road roller will cover 750 times the area covered in one revolution.
From equation (6), we have the area covered by the road roller in one revolution.
Now, the area covered by the road roller in 750 revolutions = \[750\left( 0.84\pi \right){{m}^{2}}=1980\,{{m}^{2}}\] .
Therefore, the area covered by the road roller in 750 revolutions is \[1980\,{{m}^{2}}\] .

Note: In this question, the hidden information is that the road roller is in the shape of a cylinder. Here, one might make a silly mistake while calculating the curved surface area of the road roller using the formula, \[2\pi \left( radius \right)\left( length\,of\,the\,cylinder \right)\] . In this formula, one might replace radius by 0.84 meters which is wrong because 0.84 meters is the measure of the diameter of the road roller. Therefore, to get the value of the radius we have to divide the diameter by 2.