Question

A ring of radius \[R\] is with uniformly distributed charge \[Q\] on it. A charge \[q\] is now placed at the centre of the ring. Find the increment in tension in the ring.

Answer 1

Hint:In this question, calculate the linear charge density of the ring and represent the linear charge density by \[\lambda \]. Linear charge density is directly proportional to the charge stored and inversely proportional to the circumference of the ring.

Complete step by step answerAs we know that when a charge \[ + q\] is placed at the centre of the ring, the wire gets stretched due to mutual electrostatic repulsion between the positive charge and each element of the wire having positive charge \[dQ\]. And stretching causes the internal restoring forces resulting in an additional tension in the wire of the ring.
Now we consider the figure \[\left( 1 \right)\] as,

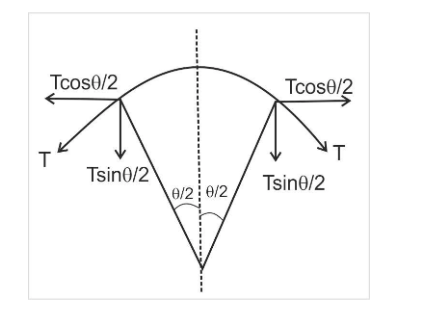
Figure\[\left( 1 \right)\]

Let us consider the linear charge density of the ring is \[\lambda \]. The linear density is the charge per unit length. Linear density tells about the charge stored in a particular area.
\[ \Rightarrow \lambda = \dfrac{Q}{{2\pi R}}\]
Where, \[Q\] is the charge \[R\] is the radius of the ring.
Now, calculate the force acting between a small section \[dx\] of the ring and the charge \[q\] in the centre will be,
\[ \Rightarrow T = \dfrac{{kq\lambda dx}}{{{R^2}}}......\left( 1 \right)\]
Where, \[T\] is the force acting in a small section of the ring.
Now consider, if \[\theta \] be the angle subtended at the center by \[dx\]. \[\theta \] is very small, and the force acting in the small section of the ring will be,
\[ \Rightarrow T\theta = 2T\sin \dfrac{\theta }{2}\]
We can write
\[ \Rightarrow \dfrac{{dx}}{R} = \theta \]
Now, we substitute the value in equation (1) as,
\[ \Rightarrow T = \dfrac{{kq\lambda \theta }}{R}\]
Therefore, the force should be equal to \[T = \dfrac{{kq\lambda \theta }}{R}\].
Now, substitute the value of \[\lambda \] in the force equation as,
\[ \Rightarrow T = \dfrac{{kq\left( {\dfrac{Q}{{2\pi R}}} \right)\theta }}{R}\]
We know that the value of $k$ is $\dfrac{1}{{4\pi {\varepsilon _0}}}$, so the equation become
\[\therefore T = \dfrac{{Qq}}{{8{\pi ^2}{\varepsilon _0}{R^2}}}\]

Therefore, the increment in the tension of the ring will be equal to \[\dfrac{{Qq}}{{8{\pi ^2}{\varepsilon _0}{R^2}}}\].

Note:As we know that, if the angle \[\theta \] be the angle subtended at the centre by \[dx\]. The angle \[\theta \] is very small, and the force acting in the small section of the ring will be equal to the charge stored in the particular area.