Question

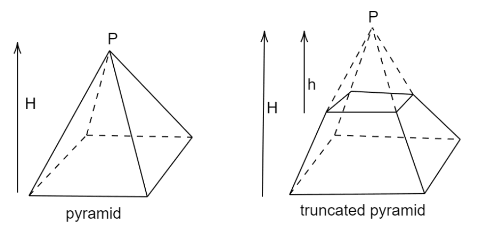
A right pyramid of square base and height $ H $ has uniform charge distributed everywhere within its volume. Modulus of electric field and potential at the apex $ P $ of the pyramid are $ {E_0} $ ​ and $ {V_0} $ ​ A symmetrical portion of height $ h $ from the apex has been removed. Find modulus of electric field and potential at the apex $ P $ of this truncated pyramid.

Answer 1

Hint: Imagine the given pyramid is made up of very small squares. Let the height of the square be unit. Find the field due to that square, we will find that the electric field will be directly proportional to length. This will give the relation between height and electric field, the potential will be square time height, find potential.

Complete Step By Step Answer:
For the given pyramid height is given $ H $ electric field at $ P $ is $ {E_0} $
And potential at $ P $ is $ {V_0} $
Now if we consider a square pyramid of unit length having electric field at its apex equals to $ E $
For unit height electric field is $ E $
Therefore for height $ H $ electric field will be $ HE $
We know $ HE = {E_0} $
So, $ E = \dfrac{{{E_0}}}{H} $
Now for second pyramid which has been cut,
 $ (H - h)E' = (H - h)\dfrac{{{E_0}}}{H} $
 $ E' = \left( {1 - \dfrac{h}{H}} \right){E_0} $
For finding potential,
 $ V = - E.dr $
 $ V $ is directly proportional to square of height.
 $ V = k{H^2} $
If $ V = {V_0} $ , $ h = H $ , then $ k = \dfrac{{{V_0}^2}}{{{H^2}}} $
 $ potential = {V_0}\left( {1 - \dfrac{{{h^2}}}{{{H^2}}}} \right) $
 $ V' = \left( {1 - \dfrac{{{h^2}}}{{{H^2}}}} \right){V_0} $
Hence, these are the electric field and potential at the apex $ P $ of this truncated pyramid.

Note:
For questions in which there is some kind of symmetry, or a part has been cut, first consider it as a whole, find the electric field or potential or whatever is to be found. Then subtract from that quantity to find electric field or potential etc. for the part which has been cut.