Question

A right angle triangle ABC is right angled at A, then the orthocenter of triangle ABC is at:
$\left( a \right)$ C
$\left( b \right)$ A
$\left( c \right)$ B
$\left( d \right)$ None of these

Answer 1

Hint: In this particular question use the concept that the orthocenter of any triangle is the intersection of the altitudes drawn from the vertices of the triangle on the opposite sides of the vertices so use these concepts to reach the solution of the question.


Complete step-by-step answer:
ABC is a right angle triangle which is right angled at A, as shown in the below figure.

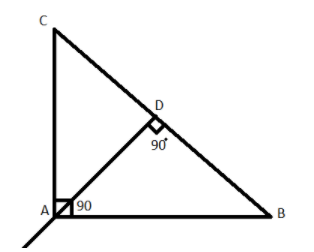
Now as we know that in a right triangle two of the sides are perpendicular to each other as shown in the above figure.
Therefore, CA is perpendicular to AB.
Now draw the perpendicular from the vertex A on the opposite side of this vertex i.e. BC as shown in the above figure which cuts the side BC at point D as shown above in the figure.
So we can say that BA, AB and AD are the altitudes from the vertices of the triangle on the opposite sides of the vertices and they intersect at point A.
Now as we all know that the orthocenter of any triangle is the intersection of the altitudes drawn from the vertices of the triangle on the opposite sides of the vertices.
So orthocenter of a right triangle is nothing but the right angle i.e. A.

Hence option (b) is the correct answer.

Note: Whenever we face such types of question the key concept we have to remember is the definition of the orthocenter of any triangle which is the basis of the solution without knowing what is the orthocenter we cannot reach to the solution so always recall the definition of the orthocenter which is stated above in the middle of the solution.