Question

A retired person wants to invest an amount of Rs. 50,000. His broker recommends investing in two types of bonds A and B yielding 10% and 9% return respectively on the invested amount. He decides to invest at least Rs. 20,000 in bond A and at least Rs. 10,000 in bond B. He also wants to invest at least as much in bond A as in bond B. Solve this linear programming graphically to maximize his returns.
A. 4900
B. 2900
C. 5400
D. 4000

Answer 1

Hint:Let the person invest x in bond A and y in bond B. Then, return in A = $\dfrac{10x}{100}$ and return in B = $\dfrac{9y}{100}$. Then the total return = $\dfrac{10x}{100}+\dfrac{9y}{100}$. Also, $x\ge 20000$, $y\ge 10000$ and $x+y\le 50000$. By solving all these equations we will try to maximize the man’s return.

Complete step-by-step answer:
It is given in the question that a retired person wants to invest an amount of Rs. 50000. If he invests in bond A, return will be 10% and if he invests in bond B, return will be 9%. Also he has to invest at least Rs. 20000 in bond A and at least Rs. 10000 in bond B. He also wants to invest at least as much amount in bond A as in bond B, so we can write $x\ge y$. Now, we have to maximize his annual return.
Let us assume that the retired person invests Rs. x in bond A and Rs. y in bond B. Now, we can calculate interest on bond A as 10% of x which is $\dfrac{10x}{100}$ and we can calculate interest on bond B as 9% of y which is $\dfrac{9y}{100}$. So, the total annual interest return will be $\dfrac{10x}{100}+\dfrac{9y}{100}=0.1x+0.09y\ldots \ldots \ldots (i)$.
He has also decided to invest at least Rs. 20000 in bond A and at least Rs. 10000 in bond B. So, we can write it as $x\ge 20000$ and $y\ge 10000$. The man has a total amount of Rs. 50000 which means that $x+y=50000\ldots \ldots \ldots (ii)$.
Let the maximum return be z and z is given by 0.1x + 0.09y, that is $z=0.1x+0.09y\ldots \ldots \ldots (ii)$.
Now, we will plot the graph. It can be done as follows.
First, we will draw a line corresponding to the condition, $x\ge 20000$, that is, its coordinate will be (20000,0), then we will draw a line for $y\ge 10000$, whose coordinate is (0,10000). The next condition is $x+y\le 50000$, in order to find the points of this line, we will first consider the value of y = 0, so we will get, $x\le 50000$ whose coordinate is (50000,0) and then we will consider x = 0, so we will get, $y\le 50000$ whose coordinate is (0,50000). Hence for the equation, $x+y\le 50000$ we get two points, (50000,0) and (0,50000). So we will mark these two points and then draw a line joining the two points. Also, we have $x\ge y$, so we will construct a line which passes through the origin.
Also, note that in all the constraints given in this question, the conditions are either (less than or equal to) or (greater than or equal to), hence while drawing the lines, we have drawn them as solid lines and not dotted lines. Dotted lines represent (less than) or (greater than) conditions.
Therefore we will get the graph as follows:

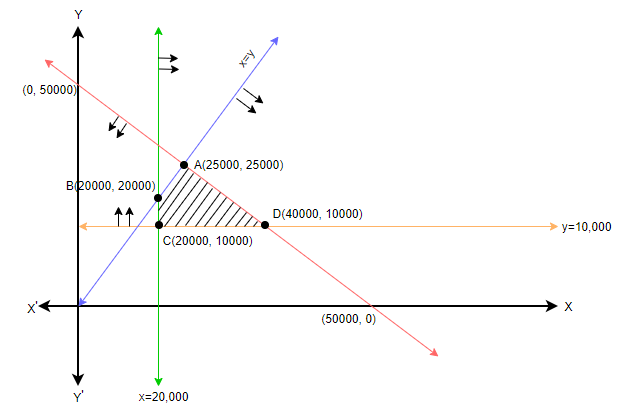
Now, we have to find the feasible region of this graph. We know that feasible region is the common region which satisfies all the given constraints and it is bound by the corner points. So, let us consider the line of each constraint.
Consider the line of the condition, $x\ge 20000$. As we can see, it is a vertical line, and we know that for a vertical line, the region towards its left satisfies the condition of less than and the region towards its right satisfies the condition of greater than. Hence the solution region of $x\ge 20000$ is the region to the right of that line.
Now, consider the line of $y\ge 10000$ and it is a horizontal line. For horizontal lines, the region above it satisfies the condition of greater than and the region below it satisfies the condition of less than. Hence, for $y\ge 10000$, the solution region is the region above that line.
Now, for $x+y\le 50000$, the region which satisfies the condition less than, will be the region below that line.
For, $x\ge y$ the region that satisfies the condition greater than, will be the region towards the right of that line.
Therefore, we get 4 corner points A, B, C and D and the feasible region is ABCD. Now we will calculate the return by plotting (x, y) in equation (iii). So, we will get:

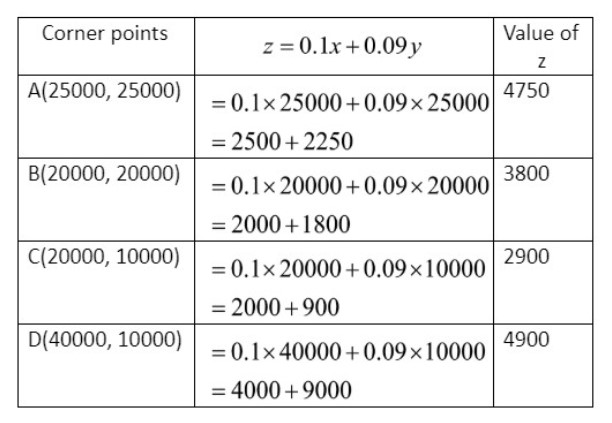
So, in order to get the maximum return the man has to invest Rs. 40000 in bond A and Rs. 10000 in bond B and the maximum return will be Rs. 4900. Hence, option (A) is the correct answer.

Note: It is recommended to plot a graph for the question of linear inequality as this will give an idea of the exact conditions of the problem. Some students tend to skip the graph and this may result in errors in their final answer. We can find the maximum and minimum value in all such questions using the graph directly.