
A resistance and inductance are connected in series with a source of alternating e.m.f. Derive an expression for resultant voltage impedance and phase difference between current and voltage in alternating circuits.
Answer
579.3k+ views
Hint: We know that voltage across the inductance \[{V_L}({V_L} = I{X_L})\] is leading voltage across the resistance \[{V_R}({V_R} = IR)\] with a phase difference of ${90^ \circ }$. We have to find the resultant of \[{V_L}\] and \[{V_R}\] to find the impedance voltage of the circuit. The relation between \[{V_L}\] and \[{V_R}\] gives the phase difference.
Complete step by step answer:
According to the question, the resistance \[R\] and the inductance \[L\] are connected in the series to an AC source which is shown in the below figure.
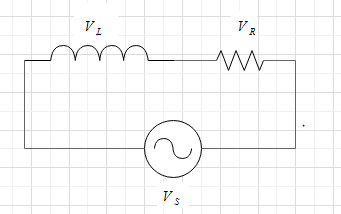
At any instance the a.c. voltage is given by-
$V = {V_0}\sin \omega t$
let \[I\] be the current which flows through the circuit.
So,
Phase difference across \[R\] will be given as ${V_R} = IR$
Phase difference across \[L\] will be given as ${V_L} = I{X_L}$
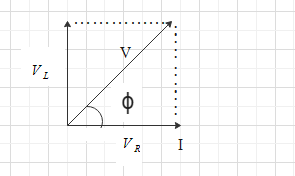
Here, we know that the \[{V_R}\] and \[I\] are in the same phase but \[{V_L}\] is leading and has a phase difference of ${90^ \circ }$.
In this way, the angle between \[{V_L}\] and \[{V_R}\] is equal to ${90^ \circ }$.
Let us find the resultant of \[{V_R}\] and \[{V_L}\] which is given by \[V\].
$
{V^2} = {V_R}^2 + {V_L}^2 \\
\Rightarrow V2 = {(IR)^2} + {(I{X_L})^2} \\
$
$
\Rightarrow {V^2} = {I^2}({R^2} + {X_L}^2) \\
\Rightarrow \dfrac{{{V^2}}}{{{I^2}}} = ({R^2} + {X_L}^2) \\
$
We have $\dfrac{V}{I} = Z$ where $Z$ is known as impedance.
So, the equation becomes-
${Z^2} = {R^2} + {X_L}^2$
or the equation can be written as $Z = \sqrt {{R^2} + {X_L}^2} $
Now, we have ${X_L} = L\omega $. Putting this value in the above equation, we get-
$Z = \sqrt {{R^2} + {L^2}{\omega ^2}} $
We know that the resultant $V$ is leading then current \[I\] flows in circuit. So,
${I_0} = \dfrac{{{V_0}}}{Z}$
or the equation will becomes,
${I_0} = \dfrac{{{V_{^0}}}}{{\sqrt {{R^2} + {L^2}{\omega ^2}} }}$
let the phase difference between \[V\] and \[I\] is $\phi $, then we have-
$\tan \phi = \dfrac{{{V_L}}}{{{V_R}}}$
Putting the values of \[{V_L}\] and \[{V_R}\] in the above equation. We get-
$\tan \phi = \dfrac{{I{X_L}}}{{IR}} = \dfrac{{{X_L}}}{R}$
So, the phase difference will be-
$\phi = {\tan ^{ - 1}}\dfrac{{{X_L}}}{R}$
So, the resultant impedance voltage is $Z = \sqrt {{R^2} + {L^2}{\omega ^2}} $and the phase difference between current and voltage is $\phi = {\tan ^{ - 1}}\dfrac{{{X_L}}}{R}$.
Note:
In a series circuit, the input current is equal to the output current while in the parallel circuit, the input voltage is equal to the output voltage. So, in the series circuit, we have to calculate the resultant voltage to find the impedance while in a parallel circuit, we have to calculate the resultant current to find the impedance. In a series circuit, the resultant voltage is a real number while in a parallel circuit the resultant current is either a real number or an imaginary number. In the series circuit, the resultant will be found in the first quadrant while in the parallel circuit, the resultant will be found in the fourth quadrant.
Complete step by step answer:
According to the question, the resistance \[R\] and the inductance \[L\] are connected in the series to an AC source which is shown in the below figure.
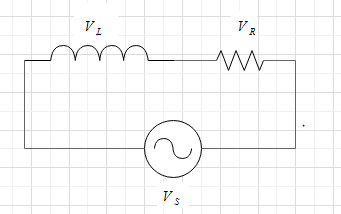

At any instance the a.c. voltage is given by-
$V = {V_0}\sin \omega t$
let \[I\] be the current which flows through the circuit.
So,
Phase difference across \[R\] will be given as ${V_R} = IR$
Phase difference across \[L\] will be given as ${V_L} = I{X_L}$
Here, we know that the \[{V_R}\] and \[I\] are in the same phase but \[{V_L}\] is leading and has a phase difference of ${90^ \circ }$.
In this way, the angle between \[{V_L}\] and \[{V_R}\] is equal to ${90^ \circ }$.
Let us find the resultant of \[{V_R}\] and \[{V_L}\] which is given by \[V\].
$
{V^2} = {V_R}^2 + {V_L}^2 \\
\Rightarrow V2 = {(IR)^2} + {(I{X_L})^2} \\
$
$
\Rightarrow {V^2} = {I^2}({R^2} + {X_L}^2) \\
\Rightarrow \dfrac{{{V^2}}}{{{I^2}}} = ({R^2} + {X_L}^2) \\
$
We have $\dfrac{V}{I} = Z$ where $Z$ is known as impedance.
So, the equation becomes-
${Z^2} = {R^2} + {X_L}^2$
or the equation can be written as $Z = \sqrt {{R^2} + {X_L}^2} $
Now, we have ${X_L} = L\omega $. Putting this value in the above equation, we get-
$Z = \sqrt {{R^2} + {L^2}{\omega ^2}} $
We know that the resultant $V$ is leading then current \[I\] flows in circuit. So,
${I_0} = \dfrac{{{V_0}}}{Z}$
or the equation will becomes,
${I_0} = \dfrac{{{V_{^0}}}}{{\sqrt {{R^2} + {L^2}{\omega ^2}} }}$
let the phase difference between \[V\] and \[I\] is $\phi $, then we have-
$\tan \phi = \dfrac{{{V_L}}}{{{V_R}}}$
Putting the values of \[{V_L}\] and \[{V_R}\] in the above equation. We get-
$\tan \phi = \dfrac{{I{X_L}}}{{IR}} = \dfrac{{{X_L}}}{R}$
So, the phase difference will be-
$\phi = {\tan ^{ - 1}}\dfrac{{{X_L}}}{R}$
So, the resultant impedance voltage is $Z = \sqrt {{R^2} + {L^2}{\omega ^2}} $and the phase difference between current and voltage is $\phi = {\tan ^{ - 1}}\dfrac{{{X_L}}}{R}$.
Note:
In a series circuit, the input current is equal to the output current while in the parallel circuit, the input voltage is equal to the output voltage. So, in the series circuit, we have to calculate the resultant voltage to find the impedance while in a parallel circuit, we have to calculate the resultant current to find the impedance. In a series circuit, the resultant voltage is a real number while in a parallel circuit the resultant current is either a real number or an imaginary number. In the series circuit, the resultant will be found in the first quadrant while in the parallel circuit, the resultant will be found in the fourth quadrant.
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Business Studies: Engaging Questions & Answers for Success

Trending doubts
Which are the Top 10 Largest Countries of the World?

What are the major means of transport Explain each class 12 social science CBSE

Draw a labelled sketch of the human eye class 12 physics CBSE

Why cannot DNA pass through cell membranes class 12 biology CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

Draw a neat and well labeled diagram of TS of ovary class 12 biology CBSE




