Question

A rectangular tank has a base that is 10 cm by 5 cm and a height of 20 cm. If the tank is half full of water, by how many centimeters will the water level rise if \[325c{m^3}\]are poured in the tank?

Answer 1

Hint: The given rectangular tank is a cuboid, so find the volume of the cuboid where volume is generally referred to as the capacity it has, or it can hold.
A rectangle has a length and width to it, and its height is multiplied to it, then it becomes a cuboid. In this question, the dimension of the tank is given, and it is filled half with, so find the volume of the half of the tank by using the volume of cuboid formula and the add the volume of rising water and then find the total height the water level will rise.

Complete step-by-step answer:
Given the half of the tank is filled with water, hence the volume of the water in the tank

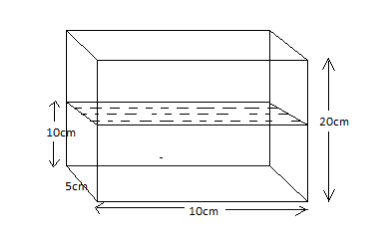
The volume of the half-filled tank
\[
  V = l \times b \times \dfrac{h}{2} \\
   = 10 \times 5 \times \dfrac{{20}}{2} \\
   = 500c{m^3} \\
 \]
Now water is added to the tank, and the volume of water increases
 \[
  V' = V + 325 \\
   = 500 + 325 \\
   = 825c{m^3} \\
 \]
Let the new level of water in the tank when \[325c{m^3}\]of water poured in the tank be\[x\], therefore

\[
  V' = l \times b \times h \\
  825 = 10 \times 5 \times x \\
  x = \dfrac{{825}}{{50}} \\
  x = 16.5cm \\
 \]
So the rise in water level will
\[
  h' = 16.5 - 10 \\
   = 6.5cm \\
 \]

Note: Students can also solve this question by finding the volume of the whole tank and dividing it with half. It will give the volume of water since only half of the tank was filled with the water and then add the volume of rising water to find the height of total water in the tank.