Question

A rectangular surface of sides $10cm$ and $15cm$ is placed inside a uniform electric field of $25V{m^{ - 1}}$, such that the surface makes an angle of $30^\circ $ with the direction of electric field. Find the flux of the electric field through the rectangular surface
$\left( A \right)0.1675\,N{m^2}{C^{ - 1}}$
$\left( B \right)0.1875\,N{m^2}{C^{ - 1}}$
$\left( C \right)Zero$
$\left( D \right)0.1075\,N{m^2}{C^{ - 1}}$

Answer 1

Hint: First we have to make a rough diagram with the help of the statement given in the problem representing all the required parameters to solve the problem. Now using the flux formula we can get the relation between the electric file area vector and the angle between the electric field and the area vector. On putting all the values we can solve the problem.

Complete answer:
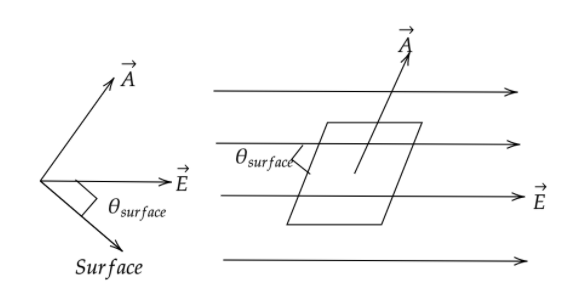
As per the problem we have a rectangular surface of sides $10cm$ and $15cm$ is placed inside a uniform electric field of $25V{m^{ - 1}}$, such that the surface makes an angle of $30^\circ $ with the direction of electric field.
Now we need to calculate the flux of the electric field through the rectangular surface.

We know,
$E = 25V{m^{ - 1}}$
Length of the rectangular surface is $10cm$ and the breadth is $15cm$.
Area of the rectangular surface will be,
$A = L \times B$
Length in meter, $L = 10 \times {10^{ - 2}}m$
Breadth in meter, $B = 15 \times {10^{ - 2}}m$
Now area will be,
$A = 10 \times {10^{ - 2}}m \times 15 \times {10^{ - 2}}m = 1.5 \times {10^{ - 2}}m$
Hence the area of the rectangular surface is,
$A = 1.5 \times {10^{ - 2}}{m^2}$
As per the figure the surface makes an angle of $30^\circ $ but we have to calculate according to the area vector which is perpendicular to the rectangular surface.
Hence the angle between the area vector and electric field lines be,
${\theta _{area}} = 90^\circ - {\theta _{surface}}$
So,
${\theta _{area}} = 90^\circ - 30^\circ = 60^\circ $
We know that flux represented as,
$\int {\phi = \int {Eda} } $
$ \Rightarrow \phi = E \cdot A = EA\cos {\theta _{area}}$
Now on putting the given values we will get,
$\phi = 25V{m^{ - 1}} \times 1.5 \times {10^{ - 2}}{m^2}\cos 60^\circ $
Hence the value of flux will be $\phi = 0.1875N{m^2}{C^{ - 1}}$.
Therefore the correct option is (B).

Note: Remember that the total electric flux out of a closed surface can also be represented as the charge enclosed divided by the permittivity. The electric flux says the number of electric lines of force intersect a given area. Note that in the problem the angle given is not the angle which is required, it is the angle between the surface and the electric field hence before putting the first calculate the correct angle that is angle between the area vector and the electric field or else you will make a mistake.