Question

A rectangular solid box of length ${\text{0}}{\text{.3 m}}$ is held horizontally, with one of its sides on the edge of a platform of height $5\;{\text{m}}$. When released, it slips off the table in a very short time $\tau = {\text{0}}{\text{.01s}}$, remaining essentially horizontal. The angle by which it would rotate when it hits the ground will be (in radians) close to:-

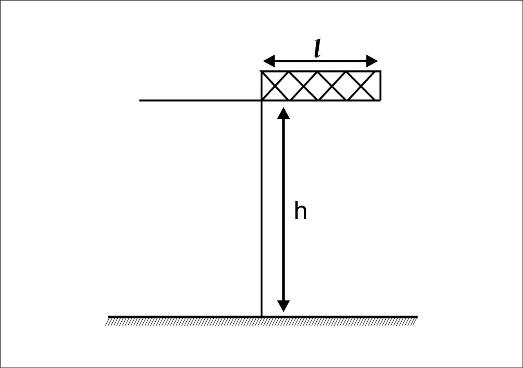
A. $0.02$
B. $0.28$
C. $0.5$
D. $0.3$

Answer 1

Hint
In this problem, first write the expression for the angular momentum in terms of torque and then in terms of angular acceleration. Then compare the expression to obtain the desired result

Complete step-by-step solution:
The Change in angular momentum of the rectangular box is given as follow
$\Delta L = \tau \Delta t$ …. (1)
Where,$\Delta t$ is the time interval and $\tau $ is the torque exerted.
But the change in angular momentum can also be given as,
$\Delta L = \dfrac{{m{l^2}}}{3}\omega $ …. (2)
Now, write the expression for the angular impulse that is torque exerted on the box as,
$\tau = mg\dfrac{l}{2}\Delta t$
Substitute the expression of torque exerted in equation (1) as,
$
  \Delta L = \tau \Delta t \\
  \Delta L = \left( {mg\dfrac{l}{2}\Delta t} \right)\Delta t \\
  \Delta L = mg\dfrac{l}{2}{\left( {\Delta t} \right)^2} \\
 $ …. (3)
Now, on equating the above equations (2) and (3) as,
$
  \dfrac{{m{l^2}}}{3}\omega = mg\dfrac{l}{2}{\left( {\Delta t} \right)^2} \\
  \omega = \dfrac{{3g}}{{2l}}{\left( {\Delta t} \right)^2} \\
 $
Now, substitute $\Delta t = 0.1\;{\text{s}}$, $g = 9.81m/sec^2$ in the above expression as shown below,
\[
  \omega = \dfrac{{3g}}{{2l}}{\left( {\Delta t} \right)^2} \\
  \omega = \dfrac{{3\left( {9.81} \right)}}{{2\left( {0.3} \right)}}{\left( {0.1} \right)^2} \\
  \omega = {\text{0}}{\text{.5 rad/s}} \\
 \]

The time taken by the rod to hit the ground is calculated as
$
  t = \dfrac{{\sqrt {2h} }}{g} \\
  t = \dfrac{{\sqrt {2\left( 5 \right)} }}{{9.81}} \\
  t \approx 1\sec \\
 $

And in this time the angle rotated by rod is calculated as,
$
  \theta = \omega t \\
  \theta = 0.5 \times 1 = {\text{0}}{\text{.5 rad}} \\
  \theta = {\text{0}}{\text{.5 rad}} \\
 $

Therefore, the correct option is C.

Note:-
Make sure that the expression for the angular momentum is correct and plug in the correct values in the expression. Make sure that the units of the quantities should be in the same unit system.