Question

A rectangular sheet of paper $44cm\times 18cm$ is rolled along its length and a cylinder is formed. The volume of the cylinder so formed is equal to (Take$\pi =\dfrac{22}{7}$ )
A.2772cm3
B.2506cm3
C.2460cm3
D.2672cm3

Answer 1

Hint: Here, in this given question, when a rectangular sheet of paper $44cm\times 18cm$ is rolled along its length and a cylinder is formed, the width of the sheet becomes the height of the cylinder and the length becomes its base circumference. Then we just need to find the value of the radius of the base of the cylinder and put it in the formula for volume of a cylinder, $\pi {{r}^{2}}h$ and get our required answer.

Complete step-by-step answer:
In this given question, a rectangular sheet of paper $44cm\times 18cm$ is rolled along its length and a cylinder is formed and we are asked to find out the volume of the formed cylinder.
Now, when a rectangular sheet of paper $44cm\times 18cm$ is rolled along its length and a cylinder is formed, the width of the sheet becomes the height of the cylinder and the length becomes its base circumference as shown in the figure.

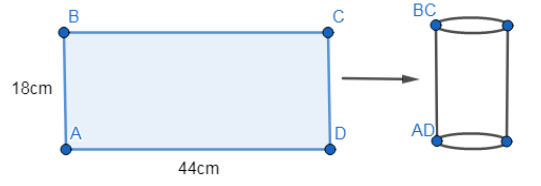
So, the height of the cylinder is 18cm.
The base circumference is equal to 44cm.
This implies that,
 $\begin{align}
  & 2\pi r=44 \\
 & \Rightarrow 2\times \dfrac{22}{7}\times r=44 \\
 & \Rightarrow r=7cm \\
\end{align}$
Now, the volume of a cylinder is equal to $\pi {{r}^{2}}h$.
So, putting the obtained value of r as 7cm in $\pi {{r}^{2}}h$, we get,
$volume=\pi {{r}^{2}}h=\dfrac{22}{7}\times {{7}^{2}}\times 18=2772c{{m}^{3}}$
Hence, we obtain the volume of the concerned cylinder as 2772cm3.
Therefore, we conclude that option (a) 2772cm3 is the correct answer to this given question.

Note: We should be careful to express the values in proper units. In this question as the length and breadth were given in terms of cm, the volume was obtained in terms of $c{{m}^{3}}$ , however, if the lengths were given in terms of other units such as meter, we should be careful to express the final answer by the corresponding units.