Question

A rectangular packing space is marked out by painting three of its sides. If the length of the unpainted side is 9 feet and the sum of the lengths of the painted sides is 37 feet, then what is the area of the packing space in square feet?
A. 46
B. 81
C. 126
D. 252

Answer 1

Hint: The two long sides are equal in length, because it is a rectangle. The area of the rectangle formed is long side length multiplied by short side length. So we get the area of the packing space.

Complete step-by-step solution:
Let ABCD be the rectangular packing space.
Let AB be the unpainted side and BC, CD and DA be the three painted sides.

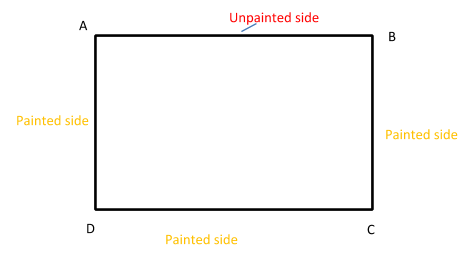
Let length of the unpainted side $AB$ be $l$.
 Also, the length of the unpainted side is given as 9 feet i.e.$AB = l = 9feet$ $AB = 9feet$
$\therefore l = 9feet$ …………(i)
The sum of the lengths of the painted sides $BC + CD + DA$ is 37 feet.
$\therefore l + 2b = 37$……………..(ii)
Now substituting the value of $l$ from (i) in (ii) we get,$\therefore l = 9feet$
$9 + 2b = 37$
Transposing 9 from L.H.S to R.H.S we get,
$2b = 37 - 9$
$ \Rightarrow 2b = 28$
Transposing 2 from L.H.S to R.H.S and converting it into its simplest form,
$b = \dfrac{{28}}{2} = 14feet$.
Now area of a rectangle= $length \times breadth$
i.e. $l \times b$………(iii)
By substituting the values of $l$and$b$in (iii) we get,
Area of the rectangle= $9 \times 14 = 126sq.ft.$
$\therefore $ The area of the packing space in square feet= $9 \times 14 = 126sq.ft.$

Hence the option C is the correct answer.

Note: The space is rectangular, so it is a rectilinear figure having four right angled intersection sides and ends. If the unpainted end is 9 feet in length, the opposite end must also be 9 feet in length. The combined length of 37 feet, which includes the 9 foot long side. Hence we can get the sum of two longer sides by simply subtracting them. Therefore the area enclosed can be calculated by simply finding the product of length and breadth as it is a rectangular space.