Question

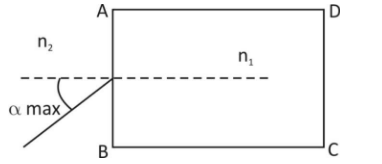
A rectangular glass slab ABCD of refractive index ${n_1},$ is immersed in water of refractive index ${n_2}\left( {{n_1} > {n_2}} \right).$ A ray of light is incident at the surface AB of the slab as shown in the figure. The maximum value of angle of incidence ${\alpha _{\max }}$such that the ray comes out only from the other surface CD, is given by

A. ${\sin ^{ - 1}}\left[ {\dfrac{{{n_1}}}{{{n_2}}}\cos \left( {{{\sin }^{ - 1}}\dfrac{{{n_2}}}{{{n_1}}}} \right)} \right]$
B. ${\sin ^{ - 1}}\left[ {{n_1}\cos \left( {{{\sin }^{ - 1}}\dfrac{1}{{{n_2}}}} \right)} \right]$
C. ${\sin ^{ - 1}}\left( {\dfrac{{{n_1}}}{{{n_2}}}} \right)$
D. ${\sin ^{ - 1}}\left( {\dfrac{{{n_2}}}{{{n_1}}}} \right)$

Answer 1

Hint:Concept of Total internal reflection is to be used. Then by shell’s law, the maximum value of $\alpha $ can be found.
Formula used:
1. Snell’s law
\[{\mu _1}\,\,\sin \,\,i\,\, = {\mu _2}\,\,\sin \,\,r\]
2. $\sin \,\,{i_C} = \dfrac{{{\mu _2}}}{{{\mu _1}}}$
Where i is the angle of incidence
R is the angle of refraction
${i_C}$ is the critical angle
The ray travel from medium having refractive index ${\mu _1}$ to medium having refractive index ${\mu _2}.$

Complete step by step answer:
 For the ray to emerge from the face CD, it has to undergo total interval reflection at face AD firstly as shown in the figure.

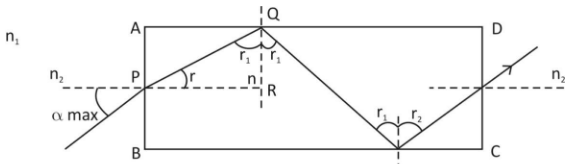
For total interval reflection to take place, angle of incidence, ${r_1} > $ critical angle ${i_C}.$
i.e. ${r_1} > {i_C}$
Now, $\sin \,\,{r_1} = \dfrac{{{n_2}}}{{{n_1}}} \Rightarrow {r_1} = {\sin ^{ - 1}}\left( {\dfrac{{{n_2}}}{{{n_1}}}} \right).......\left( 1 \right)$
Now, let corresponding ${\alpha _{\max }},$ r is the angle of redfraction
We know that,
$r + r = 90$
$ \Rightarrow r = 90 - r,$
So, $sin\,\,r = \sin \left( {90 - {r_1}} \right)$
$\sin \,\,r = \cos {r_1}\,\,\,\left( {as\,\,\cos \left( {90 - \theta } \right) = \sin \theta } \right).......\left( 2 \right)$
Now, we know that by Snell’s law the ratio of $\sin r$ (angle of incidence) to $\sin \,\,i$ (angle of refraction) is constant and gives the refractive index in case of refraction.
So, for the face AB, by applying Snell’s law, we have
${n_2}\,\,\sin \,\,{\alpha _{\max }} = {n_1}\,\,\sin \,\,r$
(as here angle of incidence $ = {\alpha _{\max }}$ and angle of refraction $ = r$) and the ray is travelling from ${n_2}$ to ${n_1}.$
Putting equation (2) in it, we get ${n_2}\,\,\sin \,\,{\alpha _{\max }} = {n_1}\,\,\cos \,\,{r_1}$
Putting ${r_1}$ from equation (1) in it,
We have
${n_2}\,\,\sin \,\,{\alpha _{\max }} = {n_1}\,\,\cos \,\left[ {{{\sin }^{ - 1}}\left( {\dfrac{{{n_2}}}{{{n_1}}}} \right)} \right]$
$ \Rightarrow \sin \,\,{\alpha _{\max }} = \dfrac{{{n_1}}}{{{n_2}}}\,\,\cos \,\left[ {{{\sin }^{ - 1}}\left( {\dfrac{{{n_2}}}{{{n_1}}}} \right)} \right]$
$ \Rightarrow {\alpha _{\max }} = {\sin ^{ - 1}}\,\left[ {\dfrac{{{n_1}}}{{{n_2}}}\cos \left( {{{\sin }^{ - 1}}} \right)\left( {\dfrac{{{n_2}}}{{{n_1}}}} \right)} \right]$
Hence, option (A) is the correct option.

Note: \[r + {r_1} = {90^0}\]
This is because $\Delta PQR,$ is a right angled triangle so,
\[r + {r_1} + {90^0} = {190^0}\] (by angle sum property)
\[r + {r_1} = {190^0} - {90^0}\]
\[ \Rightarrow r + {r_1} = {90^0}\].