Question

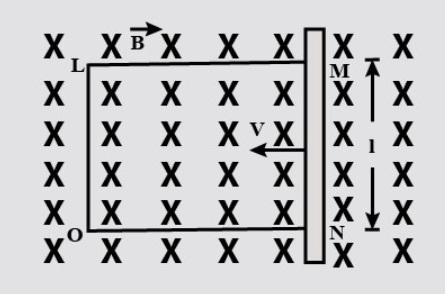
A rectangular conductor $LMNO$ is placed in a uniform magnetic field of $0.5T$ . The field is directed perpendicular to the plane of the conductor. When the arm $MN$ of length of $20cm$ is moved towards the left with a velocity of $10m{s^{ - 1}}$ calculate the emf induced in the arm. Given the resistance of the arm to be $5\Omega $ (assuming that other arms are of negligible resistance) find the value of the current in the arm.

Answer 1

Hint If a rod of length $l$ moves perpendicular to a magnetic field $B$, with a velocity $v$ , then induced emf produced in it is given by $E = Bvl$ .
The induced current is given by $I = \dfrac{E}{R}$ where $R$ is the resistance of the rod.

Complete step-by-step solution:
As from the question we can consider the arm $MN$ as a rod of length $l = 20cm$ which is moved towards left with a velocity $v = 10m{s^{ - 1}}$ perpendicular to a magnetic field $B = 0.5T$
We know from Faraday's law of induction that when flux linked with a conductor changes, an emf is induced in it.
So, to find the magnitude of emf induced along the moving rod, we use the expression from Faraday’s law of induction (only magnitude)
$E = N\dfrac{{d\phi }}{{dt}}$ where $\dfrac{{d\phi }}{{dt}}$ is the rate of change of flux
Here, $E$ implies the magnitude of the emf. In this equation, N = 1 and the flux $\phi = BA\cos \theta $ . We have $\theta = 0^\circ $ and $\cos \theta = 1$ , since $B$ is perpendicular to area $A$ . Now $d\phi = d\left( {BA} \right) = BdA$ , since $B$ is uniform. Note that the area swept out by the rod is $dA = ldx$ . Substituting these values into the expression for emf gives us
$\Rightarrow E = \dfrac{{BdA}}{{dt}} = B\dfrac{{ldx}}{{dt}}$
Finally, note that $\dfrac{{dx}}{{dt}} = v$ , the velocity of the rod. Substituting this into the last expression we have
$E = Bvl$
So, substituting the values given in the question, we have
$\Rightarrow E = 0.5 \times 0.2 \times 10 = 1V$
Now, the induced current is given by $I = \dfrac{E}{R}$ where $R$ is the resistance of the rod.
So, $I = \dfrac{1}{5} = 0.2A$ which is the final answer.

Note: We can use Lenz’s law to identify the direction of the induced field, the direction of the induced current, and the polarity of the induced emf. As the area swept by the conductor is increasing, the flux is increasing and hence the induced field must oppose the existing one and direction will be out of the page.