Question

A rectangular coil of sides $'l'$ and $'b'$ carrying current $'I'$ is subjected to a uniform magnetic field $\overrightarrow{B}$ acting perpendicular to its plane. Obtain the expression for the torque acting on it.

Answer 1

Hint: First find the area of cross-section of the coil. Then find a magnetic moment associated with the coil. From the value of the magnetic moment, calculate the torque (rotating force) acting one the dipole.

Formula used: Torque, $\tau =\text{ Force}\times \text{ perpendicular distance between the dipole}\text{.}$
Magnetic moment of the current loop, $m=NIA$, $m=\text{ magnetic moment}$ $I=\text{ Current inside the loop}$, $N=\text{ number turns of the loop}$.
Force on a current carrying conductor of length $x$ on a magnetic field $\overrightarrow{B}$ is $\overrightarrow{F}=I\left( \overrightarrow{x}\times \overrightarrow{B} \right)=Ix\left| B \right|\sin \theta $
Where $I\text{= Current inside conductor}$, $x=\text{ length of the conductor}$.
Torque, $\tau =\overrightarrow{m}\times \overrightarrow{B}=NIBA\sin \theta $

Complete step by step answer:
Area of the coil,$A=lb$
Magnetic moment associated with the coil is, $m=NIA$
Here $N=1$ so magnetic moment becomes $m=IA=Ilb$
The torque acting on the coil is given by
\[\tau =\overrightarrow{m}\times \overrightarrow{B}=mB\sin \theta \widehat{n}\] ,Where $\widehat{n}$ is the direction of torque determined by Fleming’s left hand rule. $\theta =\text{ angle between the Magnetic field and normal to the plane of coil}$.
For the given case \[\tau =\overrightarrow{m}\times \overrightarrow{B}=mB\sin \theta \widehat{n}=IlbB\sin \theta \widehat{n}\]
Here the angle between the normal and the magnetic field is $0$.

So, Torque,$\tau \text{=0}$

Additional Information: Fleming’s left hand rule states that when a current carrying conductor is placed in an external magnetic field it experiences a force which is perpendicular to the plane containing both magnetic field and flow of current. i.e. if you place your thumb, index finger and middle finger perpendicular to each other. And if the index finger represents the direction of the applied field, the middle finger represents the direction of flow of current, then the thumb will represent the force on the conductor. So the conductor will experience a force in upward direction and will try to move in that direction.

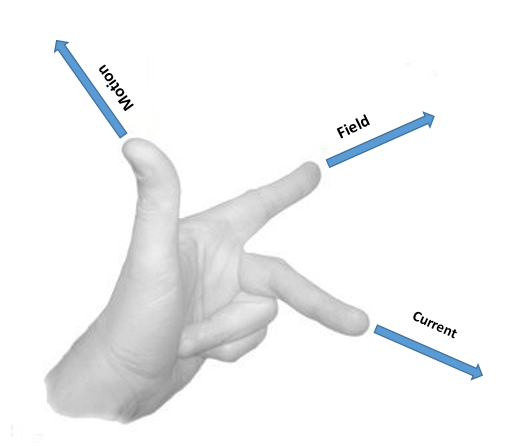
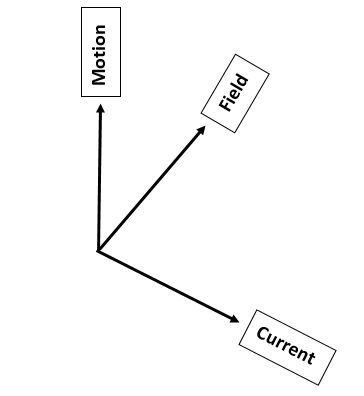
Note: The expression $\tau =NIBA\sin \theta $ holds good for planar loops of any shape. Because the torque on a current carrying loop only depends upon strength of magnetic field , number of turns of coil area of coil and current inside the coil. But is independent upon the shape of the coil.
A planar current loop of a given perimeter suspended in a magnetic field will experience maximum torque when the shape of the loop is circular, because a given perimeter circle has maximum area.