Question

A rectangular box is to be made from a sheet of 24 inch length and 9 inch width cutting out the identical square of side length x from the four corners and turning up the sides.
What is the value of x for which the volume is maximum?
A. 1 inch
B. 1.5 inch
C. 2 inch
D. 2.5 inch

Answer 1

Hint: In order to solve the problem first find the volume of the cuboidal box to be made in terms of variable x. Then finally use the property of application of derivatives. Differentiate the volume with respect to x and equate it to 0 to find the value of x.

Complete step-by-step answer:
Given that length of sheet of metal = 24 inch
Width of the sheet of metal = 9 inch
Use the figure to solve the problem.

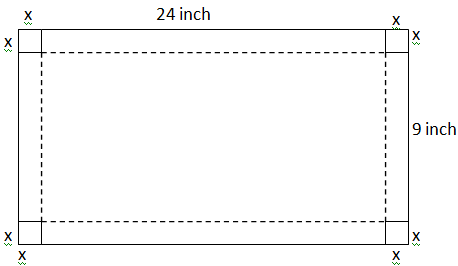
The figure shows the sheet and the dotted line shows the line from where the cuboid will be made after folding and cutting out the side square.
So after removal of the square.
Length of the cuboid $ = 24 - 2x$
Width of the cuboid $ = 9 - 2x$
Height of the cuboid $ = x$
As we know that the volume of the cuboid is given by $V = l \times b \times h$ , where v is the volume, l is the length, b is the breadth or width and h is the height.
So volume of the given cube is:
$
  \because V = l \times b \times h \\
   \Rightarrow V = \left( {24 - 2x} \right) \times \left( {9 - 2x} \right) \times x \\
 $
Let us simplify the above terms by multiplying them
\[
   \Rightarrow V = \left( {216 - 48x - 18x + 4{x^2}} \right) \times x \\
   \Rightarrow V = \left( {4{x^2} - 66x + 216} \right) \times x \\
   \Rightarrow V = 4{x^3} - 66{x^2} + 216x..........(1) \\
 \]
As we know the application of derivatives in finding the maxima.
To find the maxima of any function we differentiate the function and equate it with 0.
So to know the volume maximum $\dfrac{{dV}}{{dx}} = 0$
So let us differentiate the equation of volume which is given by equation (1).
$ \Rightarrow \dfrac{{dV}}{{dx}} = \dfrac{d}{{dx}}\left[ {4{x^3} - 66{x^2} + 216x} \right] = 0$
Now let us differentiate the terms separately by the use of properties of differentiation.
$
   \Rightarrow \dfrac{d}{{dx}}\left[ {4{x^3} - 66{x^2} + 216x} \right] = 0 \\
   \Rightarrow \dfrac{d}{{dx}}\left( {4{x^3}} \right) + \dfrac{d}{{dx}}\left( { - 66{x^2}} \right) + \dfrac{d}{{dx}}\left( {216x} \right) = 0 \\
   \Rightarrow 4\dfrac{d}{{dx}}\left( {{x^3}} \right) - 66\dfrac{d}{{dx}}\left( {{x^2}} \right) + 216\dfrac{d}{{dx}}\left( x \right) = 0 \\
 $
As we know that
$\dfrac{d}{{dx}}\left( {{x^n}} \right) = n{x^{n - 1}}$
Using the formula in the above equation we get:
$
   \Rightarrow 4\left( {3{x^2}} \right) - 66\left( {2x} \right) + 216\left( 1 \right) = 0 \\
   \Rightarrow 12{x^2} - 132x + 216 = 0 \\
 $
Now let us solve the quadratic equation in order to find the value of x.
First we will take 12 common and then split the middle term.
$
   \Rightarrow 12\left( {{x^2} - 11x + 18} \right) = 0 \\
   \Rightarrow {x^2} - 11x + 18 = 0 \\
   \Rightarrow {x^2} - 9x - 2x + 18 = 0 \\
   \Rightarrow \left( {x - 9} \right) - 2\left( {x - 9} \right) = 0 \\
   \Rightarrow \left( {x - 2} \right)\left( {x - 9} \right) = 0 \\
   \Rightarrow x = 2{\text{ or }}x = 9 \\
 $
Let us substitute the value of x as 2 and 9 in the equation of volume.
For x = 2
Volume
\[
  V = 4{\left( 2 \right)^3} - 66{\left( 2 \right)^2} + 216\left( 2 \right) \\
  V = 32 - 264 + 432 \\
  V = 200c{m^3} \\
 \]
For x = 9
Volume
\[
  V = 4{\left( 9 \right)^3} - 66{\left( 9 \right)^2} + 216\left( 9 \right) \\
  V = 2916 - 5346 + 1944 \\
  V = - 486c{m^3} \\
 \]
As for x=9 we get negative volume so x = 2 is the correct answer.
Hence, the value of x for which the volume is maximum is 2 inch.
So, option C is the correct option.

Note: In order to solve such types of problems students must remember the formula for volume of some common shapes such as cuboid. Also students must remember the method of finding maxima and minima from the function by the use of derivatives.