Question

A rectangle ABCD is inscribed in a circle with a diameter lying along the line 3y = x + 10. If A and B are the points (-6,7) and (4,7) respectively then
${\text{A}}{\text{. }}$ centre of the circle is ( -1,3)
${\text{B}}{\text{.}}$ centre of the circle is ( -1,0 )
${\text{C}}{\text{.}}$ area of the rectangle is 100 sq. units
${\text{D}}{\text{. }}$ area of the rectangle is 80 sq. units

Answer 1

Hint: Proceed by finding the centre of the circle, assumed to be $\left( {h,k} \right)$ , by taking one of the points A or B on the line equation given. Get one more equation and get the centre. For finding the area of the rectangle, get the adjacent sides of the rectangle by using distance formula in AB and use the radius of the circle to get BC.

Complete step-by-step answer:
Let the centre of the circle be O(h,k) and the given equation of line is the diameter of the circle which means the centre lies on this line and satisfies the equation of the line,
              3k = h + 10
              3k – 10 = h..... eq.1

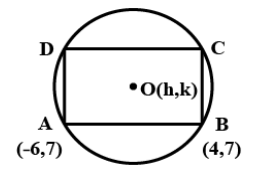
Since, OA = OB (as they both are equal to the radii of the circle)
$
  {\left( {h + 6} \right)^2} = {\left( {h - 4} \right)^2} \\
  {h^2} + 36 + 12h = {h^2} + 16 - 8h \\
  20 = - 20h \\
  h = - 1 \\
$
From eq. 1, we can get k as 3.
So, h = -1 and k = 3
Therefore, the centre of the circle is $\left( { - 1,3} \right)$.
In order to find the area of the rectangle, we need to find the two adjacent sides of the rectangle.
In the question, we are given the points A and B. From these, we can determine the length AB.
$
   = \sqrt {{{\left( { - 6 - 4} \right)}^2} + {{\left( {7 - 7} \right)}^2}} \\
   = \sqrt {100} \\
   = 10 \\
 $
To find BC, let’s find AC first. Then we can apply Pythagora's theorem in the triangle ABC.
$A{C^2} = A{B^2} + B{C^2}$
AC is the diameter.
AC = 2R where R is the radius.
R will be the distance between point A and the centre O.
$
  \sqrt {{{\left( {6 - 1} \right)}^2} + {{\left( { - 7 + 3} \right)}^2}} \\
  \sqrt {25 + 16} \\
  R = \sqrt {41} \\
  {\text{diameter}} = 2\sqrt {41} \\
$
$
  AC = 2\sqrt {41} \\
  AB = 10 \\
 $
$
  A{C^2} = A{B^2} + B{C^2} \\
  {\left( {2\sqrt {41} } \right)^2} = {10^2} + B{C^2} \\
  164 = 100 + B{C^2} \\
  64 = B{C^2} \\
  8 = BC \\
 $
Area of the rectangle will be AB x BC
So, 10 x 8 = 80 sq. Units
The correct options are A and D.

Note: Finding the second equation while solving for the centre of the circle, by taking equidistant method from centre of the circle and the two points A and B is an important approach since the same concept is used in many numerical f conic sections.