Question

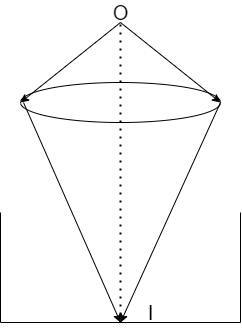
A real image of an object is formed by a convex lens at the bottom of an empty beaker. The beaker is now filled with a liquid of refractive index $1.4$ to a depth of $7cm$. In order to get the image at the bottom, the beaker should be moved

A) Downward by $2cm$
B) Upward by $2cm$
C) Downward by $3cm$
D) Upward by $3cm$

Answer 1

Hint: Refraction is defined as the phenomenon of bending of light rays. When the light rays travel from one medium to the other medium of different refractive index and densities, then the ray of light bends. It changes the wavelength and the speed of light.

Complete step by step answer:
Given that the beaker was empty but later on it was filled with a liquid. When the light rays strike on the surface of the liquid, then they bend and the image of the object will appear to be at some point the bottom of the beaker below point I.
The light rays follow Snell’s Law. According to this law, for a given pair of mediums, the ratio of sine of angle of incidence to the sine of angle of refraction is constant. It is written as:
$\dfrac{{\sin i}}{{\sin r}} = \mu $
Where $\mu $is the constant. It is called the refractive index of the second medium with respect to first.
When an observer and the object are in two different mediums, then the image of the object seems like it has been shifted from its normal position. It is known as normal shift.
It’s formula is
$d = t(1 - \dfrac{1}{\mu })$
The thickness of the liquid is $t = 7cm$
The refractive index is $\mu = 1.4$
Substituting the given values in the formula and solving,
$\Rightarrow d = 7(1 - \dfrac{1}{{1.4}})$
On simplification,
$\Rightarrow d = 7(1 - 0.71)$
On further simplification,
$\Rightarrow d = 7 \times 0.29$
$\Rightarrow d = 2.03 \approx 2cm$

The image at the bottom of the beaker should be moved downwards by $2cm$. Therefore Option A is the right answer.

Note:
It is to be noted that there is a difference between the terms lateral shift and normal shift. Lateral shift is defined as the perpendicular distance between the incident and the emergent rays. But normal shift is the shifting in the position of the object.