Question

A ray of light passes through an equilateral prism such that the angle of incidence is equal to the angle of emergence and each of these equal to $\dfrac{3}{4}$ of the angle of the prism. The angle of deviation is
(A) $45^\circ $
(B) $39^\circ $
(C) $20^\circ $
(D) $30^\circ $

Answer 1

Hint:When a ray of light passes through a prism, it gets refracted at the surfaces and the final ray comes out of the prism after the last refraction. If the prism was not present, the ray would have traced the straight path, but due to the prism it got deviated. The angle by which the ray deviates is called as the angle of deviation. Consider a prism, incident a light ray on it and trace the path of the light. By applying geometry, you can find the angle of deviation.

Complete step by step solution:

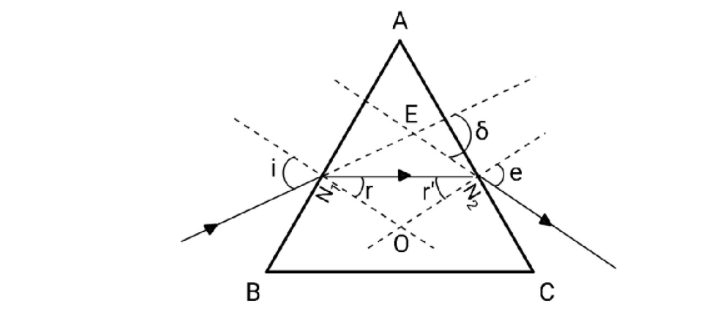
Consider this cross section of equilateral prism, the ray refracts at the point ${N_1}$ on surface AB, it then travels and hits the point ${N_2}$ on surface AC and again gets refracted.
From the exterior angle property, which states that the exterior angle is sum of the two opposite interior angles, we have
$\delta = \angle E{N_1}{N_2} + \angle E{N_2}{N_1}$
As you can see, $\angle E{N_1}O$ and $i$ are opposite angles and hence they are equal.
$\therefore \angle E{N_1}O = i = \angle E{N_1}{N_2} + r$
Similarly,

$\therefore \angle E{N_2}O = e = \angle E{N_2}{N_1} + r'$, $e$ is the angle of emergence and $r\&
r'$ are the angle of refractions.
Substituting values of $\angle E{N_1}{N_2}\& \angle E{N_2}{N_1}$ from the above equations in the
equation of $\delta $,
$
\delta = \left( {i - r} \right) + \left( {e - r'} \right) \\
\delta = \left( {i + e} \right) - \left( {r + r'} \right) \\
$
Now consider the quadrilateral $A{N_1}O{N_2}$, since the lines drawn from ${N_1}\& {N_2}$ are
perpendicular to the surfaces , we have $\angle A{N_1}O = \angle A{N_2}O = 90^\circ $
The sum of angles of a quadrilateral add up to $360^\circ $$\angle A{N_1}O = \angle A{N_2}O =
90^\circ $,
$
\therefore A + \angle {N_1}O{N_2} + 90^\circ + 90^\circ = 360^\circ \\
\therefore A + \angle {N_1}O{N_2} = 180^\circ \\
$
Here, $A$ is the angle of prism.
In triangle $\Delta {N_1}O{N_2}$,
$
\angle {N_1}O{N_2} + r + r' = 180^\circ \\
\therefore \angle {N_1}O{N_2} = 180^\circ - \left( {r + r'} \right) \\
$
Substituting this value in equation of $A$
$
A + 180^\circ - \left( {r + r'} \right) = 180^\circ \\
\therefore A = \left( {r + r'} \right) \\
$
Substituting value of $A$ from the above equation in the equation of $\delta $,
$\delta = i + e - A$.
This is how the angle of deviation is given.
Now, given data are as follows:

The triangle is an equilateral triangle, $\therefore A = 60^\circ $, the angle of incidence is equal to
the angle of emergence, $\therefore i = e$ and each of these angles are $\dfrac{3}{4}$ of the angle
of prism, $\therefore i = e = \dfrac{3}{4}A$
$
\delta = i + i - A \\
\therefore \delta = 2i - A \\
\therefore \delta = \left( 2 \right)\dfrac{3}{4}A - A \\
\therefore \delta = \dfrac{A}{2} \\
$
$
\therefore \delta = \dfrac{{60^\circ }}{2} \\
\therefore \delta = 30^\circ \\
$
Hence, the angle of deviation is $30^\circ $

Option (B) is correct.

Note: Always track the light ray to obtain an equation related to the problem. Also remember that the ray refracted at surface AB is not necessarily parallel to line BC, it can be in another direction.Keep in mind the different basic properties and theorems in geometry. Focus on how we reached the final destination.