Question

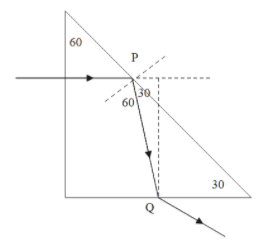
A ray of light is incident normally on one face of a prism as shown in figure. The refractive index of the material of the prism is $\dfrac{5}{3}$ ​ and the prism is immersed in water of refractive index $\dfrac{4}{3}$ ​ then

A) the angle of emergence of the ray is ${{\sin }^{-1}}(\dfrac{5}{8})$
B) the angle of emergence of the ray is ${{\sin }^{-1}}(\dfrac{5}{4\sqrt{3}})$
C) the angle of emergence of the ray is ${{\sin }^{-1}}(\dfrac{7}{3\sqrt{4}})$
D) TIR will not occur at p if the refractive index of water increases to a value greater than $\dfrac{5}{2\sqrt{3}}$ by dissolving some substance.

Answer 1

Hint: Snell’s law can be used to solve the above problem. As total internal reflection is occurring at point p, use snell's law to find out the angle of emergence. Next, check the angle of emergence when the refractive index is changed. If it follows the total internal reflection rule, then TIR is possible.

Formulas used:
${{\mu }_{1}}\sin {{\theta }_{1}}={{\mu }_{2}}\sin {{\theta }_{2}}$

Complete answer:
If we check the diagram above, in the first case when the refractive index of the water isn’t changed,
The total internal reflection doesn’t occur at point p.
Therefore, using snell's law,
$\begin{align}
  & {{\mu }_{1}}\sin {{\theta }_{1}}={{\mu }_{2}}\sin {{\theta }_{2}} \\
 & \dfrac{5}{3}\sin {{30}^{0}}=\dfrac{4}{3}\sin {{\theta }_{2}} \\
 & {{\theta }_{2}}={{\sin }^{-1}}(\dfrac{5}{8}) \\
\end{align}$

Therefore, the angle of emergence when the refractive index of water isn’t changed is option a.
Now, when the refractive index of water is changed to new one by dissolving some substance,
$\begin{align}
  & {{\mu }_{w}} > \dfrac{5}{2\sqrt{3}} \\
 & \sin C > \dfrac{5}{2\sqrt{3}}\times \dfrac{3}{2} \\
 & C > {{60}^{0}} \\
\end{align}$
As we can see, there’s no possibility of total internal reflection here. Therefore, the correct option is d.

Finally, the correct options are a, d.

Additional information:
When light is incident upon a medium of lesser index of refraction, ray is bent away from the normal. This means that the exit angle is greater than the incident angle. This phenomenon is called internal reflection. If in case, the exit angle is equal to ninety degrees or greater than ninety degrees, the critical angle will be total internal reflection. Snell's law is used to calculate the critical angle. If the angle of incidence is less than the critical angle, some part of incident light will be transmitted and part will be reflected back.

Note:
If the angle of incidence of a ray is less than the critical angle, the ray neither gets reflected completely nor gets transmitted completely. Some part of the ray transmits and some part of the ray reflects. If the incident angle is greater than the critical angle, we can see total internal reflection.