Question

A ray of light from denser medium strikes a rarer medium at an angle of incidence$i$. The reflected and refracted rays make an angle of $\dfrac{\pi }{2}$with each other. If the angles of reflection and refraction are r and r’, then the critical angle will be:
A. ${\tan ^{ - 1}}(\sin i)$
B. ${\sin ^{ - 1}}(\sin r)$
C. ${\sin ^{ - 1}}(\tan i)$
D. ${\sin ^{ - 1}}(\tan r)$

Answer 1

Hint:Snell’s law is a law which states that the ratio of the sines of the angles of incidence and refraction of a wave is constant when it passes between two given media. Or in other words, we can say Snell's law is a formula used to describe the relationship between the angles of incidence and refraction, when referring to light or other waves passing through a boundary between two different isotropic media, such as water, glass, or air. The relationship is something like this: \[n1\sin \theta 1 = n2\sin \theta 2\]
The critical angle is the angle of incidence where the angle of refraction is${90^ \circ }$. For this, the light must travel from optically denser to a rarer medium.

Complete step by step solution:

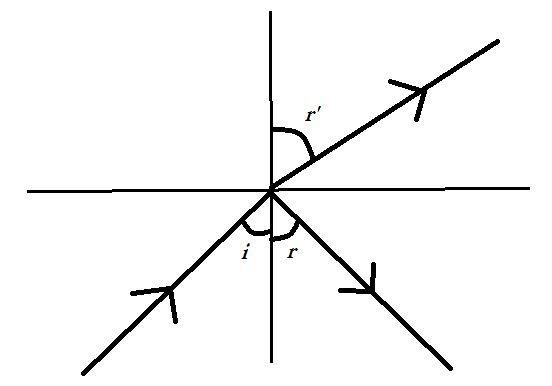
Let $\mu 1$ be the refractive index of a rarer medium and $\mu 2$be the refractive index of the denser medium.
According to the question:
$i$is the angle of incidence; $r$is the angle of reflection and $r'$is the angle of refraction.
And angle between angle of reflection and angle of refraction is $\dfrac{\pi }{2}$
$\begin{gathered}
  r + r' = \dfrac{\pi }{2} \\
   \Rightarrow r' = \dfrac{\pi }{2} - r \\
\end{gathered} $
Let the required critical angle be C. then,
$\begin{gathered}
  This \Rightarrow \mu 1\sin C = \mu 2 \\
   \Rightarrow \sin C = \dfrac{{\mu 2}}{{\mu 1}} \\
\end{gathered} $


Now applying snell’s law,
\[\begin{gathered}
  \mu 1\sin i = \mu 2\sin r' \\
   \Rightarrow \dfrac{{\mu 2}}{{\mu 1}} = \dfrac{{\sin i}}{{\sin r'}} \\
   \Rightarrow \sin C = \dfrac{{\sin i}}{{\sin r'}} \\
   \Rightarrow \sin C = \dfrac{{\sin i}}{{\sin (\dfrac{\pi }{2} - r)}} \\
   \Rightarrow \sin C = \dfrac{{\sin i}}{{\cos r}} \\
   \Rightarrow \sin C = \dfrac{{\sin i}}{{\cos i}} \\
   \Rightarrow \sin C = \tan i \\
   \Rightarrow C = {\sin ^{ - 1}}(\tan i) \\
\end{gathered} \]

Hence the required critical angle is \[C = {\sin ^{ - 1}}(\tan i)\]

Note:Always note that to find the critical angle the light must be travelling from optically denser to a rarer medium. Be careful while applying snell’s law.