Question

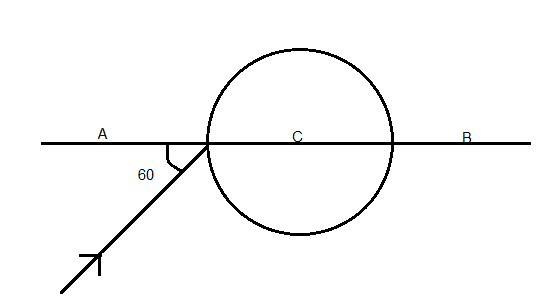
A ray of light falls on a transparent sphere with centre at C is shown in Fig.
The ray emerges from the sphere parallel to line AB. The refractive index of the sphere is
1- \[\sqrt{2}\]
2- \[\sqrt{3}\]
3- \[\dfrac{3}{2}\]
4- \[\dfrac{1}{2}\]

Answer 1

Hint: If a ray is incident obliquely that is perpendicular to the glass surface then it moves in to the second medium undeviated. But when it falls at some angle and if the medium changes then the path changes and it can be determined by using Snell’s law. In order to apply Snell’s law, we have to draw a normal at the point of incidence.

Complete step by step answer:
From Snell’s law, \[\mu =\dfrac{\sin i}{\sin r}\]

\[\begin{align}
  & \mu =\dfrac{\sin i}{\sin r} \\
 & \Rightarrow \mu \sin r=\sin i \\
\end{align}\]
\[\Rightarrow \mu \sin r=\sin i\]--(1)

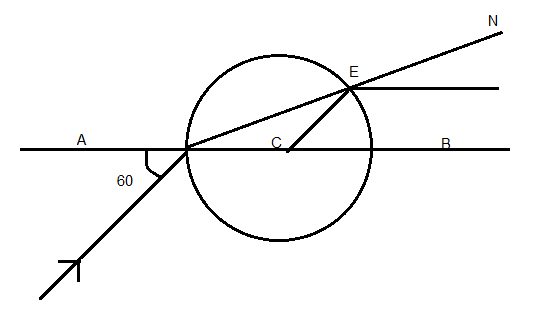
Since perpendicular at any point on a circle passes through the center, CN is normal at E
So, angle D= angle E
From the exterior angle property, angle BCE = 2r
From Snell’s law, \[\mu =\dfrac{\sin i}{\sin r}\]
\[\Rightarrow \mu \sin r=\sin 2r\]----(2)
Using eq (1) the LHS, we get, sin i= sin 2r
\[\begin{align}
  & \sin i=\sin 2r \\
 & \sin 60=\sin 2r \\
 & 60=2r \\
 & r={{30}^{0}} \\
\end{align}\]
\[\Rightarrow r={{30}^{0}}\]
From Snell’s law, \[\mu =\dfrac{\sin i}{\sin r}\]
\[\Rightarrow \mu =\dfrac{\sin 60}{\begin{align}
  & \sin 30 \\
 & \\
\end{align}}\]
\[\Rightarrow \mu =\sqrt{3}\]

So, the correct answer is “Option 2”.

Note:
while using snell's law the refractive index is given by the ratio of refractive of the refractive index of the second medium to the refractive index of first medium. Be careful while the angles of reflection, refraction and of incidence are always made with the normal. The refractive index of vacuum or air is unity and when we talk about relative refractive index then we take the ratio of the refractive index of a given medium with respect to unity.