Question

A radio wave of frequency 90MHZ (FM) enter into a ferrite rod. If ${\varepsilon _r} = {10^3}{\text{ and }}{\mu _r} = 10,$ then the velocity and the wavelength radio wave in ferrite rod are:
$\eqalign{
  & (A)3 \times {10^6}m{s^{ - 1}},3.33 \times {10^{ - 2}}m \cr
  & (B)3 \times {10^5}m{s^{ - 1}},3.33 \times {10^{ - 1}}m \cr
  & \left( C \right)3 \times {10^6}m{s^{ - 1}},3.33 \times {10^{ - 3}}m \cr
  & (D)3 \times {10^5}m{s^{ - 1}},3.33 \times {10^{ - 2}}m \cr} $

Answer 1

Hint: By using permittivity and permeability values, we will find out the velocity of the radio wave in the ferrite rod. Then we will use the relation between the velocity and the wavelength; And finally using this relation we will calculate the wavelength of the radio wave for the required answer.

Formula used:
$\eqalign{
  & \gamma = \dfrac{c}{{\sqrt {{\varepsilon _r}{\mu _r}} }} \cr
  & \lambda = \dfrac{c}{\gamma } \cr} $

Complete solution:
We know that the radio waves are a type of electromagnetic radiation best known for their use in communication technologies, such as television, mobile phones and radios. These devices receive radio waves and convert them into mechanical vibrations in the speakers to create sound waves.

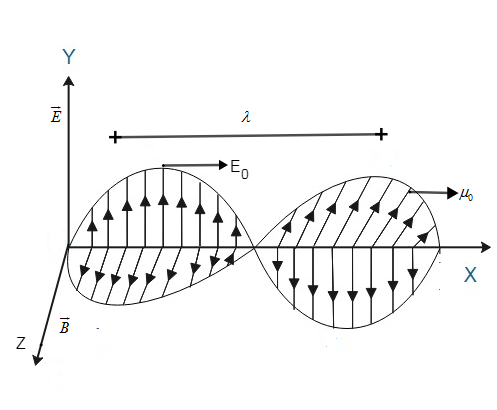
As we know that velocity of EM waves is same as the speed of light that is $c = 3 \times {10^8}m/s$ as shown in diagram, $\overrightarrow \varepsilon $ is the electrical field along y-axis and $\overrightarrow B $ is the magnetic field along z-axis. ${\varepsilon _0}$is the permittivity and ${\mu _0}$ is the permeability of the medium used for the propagation of waves. According to the question ${\varepsilon _o} = {10^3},{\mu _r} = 10$now find the velocity of radio wave in ferrite rod is: $\gamma = \dfrac{c}{{\sqrt {{\varepsilon _r}{\mu _r}} }}$. Putting values we get
$\eqalign{
  & \gamma = \dfrac{{3 \times {{10}^8}}}{{\sqrt {{{10}^3} \times 10} }} = \dfrac{{3 \times {{10}^8}}}{{\sqrt {{{10}^4}} }} \cr
  & \gamma = \dfrac{{3 \times {{10}^8}}}{{{{10}^2}}} \cr
  & \Rightarrow \gamma = 3 \times {10^6}m/s \cr} $
Now to wavelength of radio wave use the relation $\lambda = \dfrac{c}{\gamma }$
We know that
$c = 3 \times {10^8}m/s,\gamma = 90 \times {10^6}m/s$
Substituting these values in the above equation we get:
$\eqalign{
  & \lambda = \dfrac{{3 \times {{10}^8}}}{{90 \times {{10}^6}}} \cr
  & \Rightarrow \lambda = \dfrac{{{{10}^8}}}{{{{10}^6}}} \times \dfrac{1}{{30}} \cr
  & \Rightarrow \lambda = 0.333 \times {10^{ - 1}} \cr
  & \therefore \lambda = 3.33 \times {10^{ - 2}}m \cr} $
Hence, the velocity and the wavelength radio wave in ferrite rod are $3 \times {10^6}m{s^{ - 1}},3.33 \times {10^{ - 2}}m$ respectively.

Therefore the correct option for the given question is (a).

Note:
Radio waves are kind of electromagnetic waves and thus they travel with the speed of light radio waves travel very quickly through space. A radio wave is generated by a transmitter and detected by a receiver.