Question

What is a quadrilateral that has exactly 2 congruent consecutive sides? Would it be either a parallelogram and/or a trapezoid?

Answer 1

Hint: We first explain the concept of congruent consecutive sides. Then we take the given options individually and explain if they satisfy the conditions. We give proper reasons against every form of quadrilateral.

Complete step by step solution:
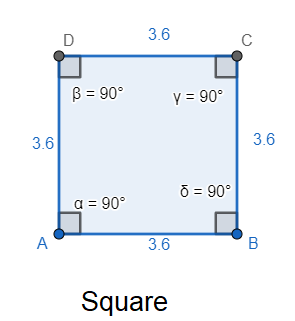
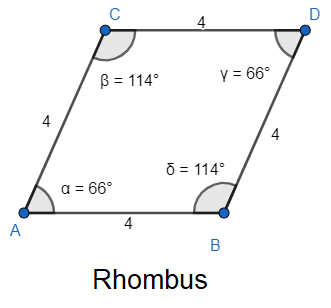
A parallelogram can be defined in the form of a quadrilateral which has its opposite sides parallel or equal or both. It has no particular condition of consecutive sides being congruent to each other. If the consecutive sides of parallelogram are equal then it becomes a particular form of parallelogram which is rhombus. Since a square, a rhombus and a rectangle are also parallelograms, they are also excluded.

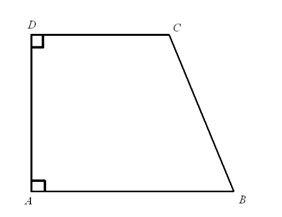
In a trapezoid if the bases are congruent to one and only one of the adjacent sides then the condition is satisfied. We are excluding the concept of isosceles trapezoid.

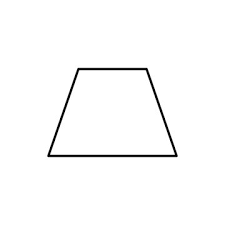
In the case of trapezium, for the basic restrictions of a generic quadrilateral, it is possible to make two consecutive sides congruent to each other and make the two other sides different from each other and of the first two sides. So, for such a special kind of trapezium, the condition is satisfied.

Note: The concept of congruent and regular is different. The concept of irregular quadrilateral comes from congruent sides and angles being not equal. This is different from being congruent.