Question

A property dealer sells a site for \[6,30,000\] and makes a profit of \[5\% \]. Had he sold it for \[5,00,000\], then the percentage of profit or loss he would have made is
A.\[2\dfrac{1}{4}\% \] gain
B.\[10\% \] loss
C.\[12\dfrac{1}{2}\% \] loss
D.\[16\dfrac{2}{3}\% \] loss

Answer 1

Hint: The given question is based on profit and loss values. For solving the question, profit and loss identities are to be applied. Firstly, we will find the cost price of the given question, then apply the loss identity to find out the value of loss. Then apply the loss percentage identity to find the loss percentage of the given question. By using all the identities, we can find how much is the loss percentage and profit percentage in the given question.

Complete step-by-step answer:
 The given question is based on selling price and cost price of a property.
Selling price is defined as the price at which a good or service is sold by the seller to the buyer.
Cost price is the original price of an item. The cost is the total outlay required to produce a product or carry out a service.
As the selling price of the property is \[6,30,000\]
We have given profit \[ = 5\% \]
We have to find the cost price \[ = \dfrac{{100}}{{105}} \times 6,30,000\]
Solving the above equation by multiplying \[ = 100 \times 6,30,000\], we get \[6,30,00,000\]
\[ = \dfrac{{6,30,00,000}}{{105}}\]
Now, solve the above term by dividing; we get,
Cost price \[ = 6,00,000\]
The cost price of the property is \[6,00,000\]
As given that the property sold for \[5,00,000\]
Finding the value of loss by using identity: \[Loss{\text{ }} = {\text{ }}C.P{\text{ }}-{\text{ }}S.P\;.........(A)\]
Where C.P is the cost price and S.P is the selling price
Substituting the value of C.P i.e., \[6,00,000\] and S.P i.e., \[5,00,000\] in identity (A), it becomes.
Loss \[ = 6,00,000 - 5,00,000\]
Loss \[ = 1,00,000\]
The value of loss is \[1,00,000\]
Now, finding the percentage of loss by using identity:
\[Loss\% = \dfrac{{loss}}{{C.P}} \times 100 \ldots \ldots .\left( B \right)\]
Substituting the value of loss and C.P in the above identity (B), it becomes
Loss % \[ = \dfrac{{1,00,000}}{{6,00,000}} \times 100\]
Multiplying \[1,00,000\] by \[100\], we get \[1,00,00,000\]
\[Loss{\text{ }}\% = \dfrac{{1,00,00,000}}{{6,00,000}}\]
Dividing the above term, we get \[\dfrac{{100}}{6}\]
Again, we divide \[100\] by \[6\] as

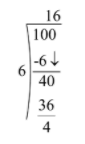
By using the rule, \[Q\dfrac{R}{P}\], where \[Q\] is quotient, \[R\] is remainder and \[D\] is divisor. So, it can be written as \[16\dfrac{4}{6}\]
As \[\dfrac{4}{6}\] can be simplified by dividing it by \[2\], we will get it as \[\dfrac{2}{3}\]. Now, the term becomes:
\[16\dfrac{2}{3}\]
So, from the given question, the loss is \[16\dfrac{2}{3}\% \].

Note: The above question is based on profit and loss terms. The identity of loss and profit is to be used for solving the problem. The identity is used in mathematics to determine the price of a commodity in the market. To understand how profitable a business is, we find the profit and loss percentage of it.