Question

A projectile thrown with velocity $v$ making an angle $\theta $ with the vertical gains a maximum height $H$ in the time of its flight. The time for which the projectile remains in the air is:
$A)\text{ }\sqrt{\dfrac{H\cos \theta }{g}}$
$B)\text{ }\sqrt{\dfrac{2H\cos \theta }{g}}$
$C)\text{ }\sqrt{\dfrac{4H}{g}}$
$D)\text{ }\sqrt{\dfrac{8H}{g}}$

Answer 1

Hint: This problem can be easily solved by considering the emotion of the projectile in only one axis, that is, the vertical axis where it faces a constant downward acceleration, that is, the acceleration due to gravity. From the initial velocity given and the angle made with the vertical we can find out the initial velocity of the projectile in the upward direction.

Formula used:
$s=ut+\dfrac{1}{2}a{{t}^{2}}$
$PE=mgH$
$KE=\dfrac{1}{2}m{{v}^{2}}$

Complete step-by-step answer:
We will solve for the motion of the projectile only in the vertical axis and hence, the problem becomes a problem of motion in one dimension. The time for which the body remains in motion in the vertical direction will essentially be the time of flight of the projectile.
In the vertical direction, the project is subjected to a constant downward acceleration equal to the acceleration due to gravity $g$.
Now, for motion with constant acceleration $a$, the displacement $s$, initial velocity $u$ and time interval $t$ is given by
$s=ut+\dfrac{1}{2}a{{t}^{2}}$ --(1)
Now, let us analyze the question.
We shall consider the motion of the body till it reaches the maximum height and find out the time required for it. The same time will be taken by the projectile for its downward journey and hence, we can find out the total time of flight by doubling the time taken for reaching the maximum height.
The acceleration of the body in the vertical axis is $g$.
The displacement of the projectile is the maximum height equal to $H$.
The initial velocity is ${{v}_{y}}$.
Let the time taken be $t$.
Now, we shall attempt to find ${{v}_{y}}$.
It is given that the initial velocity of the projectile is $v$ and it makes an angle $\theta $ with the vertical. Let us draw a figure depicting the situation.

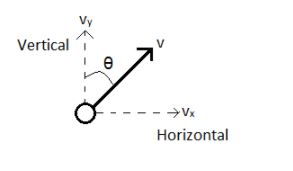
From the figure, we can see that by geometry
${{v}_{y}}=v\cos \theta $ --(2)
Now using (1), we get
$H={{v}_{y}}t-\dfrac{1}{2}g{{t}^{2}}$
The negative value of acceleration implies that $g$ acts in the downward direction.
Putting (2) in the above equation, we get
$H=v\cos \theta t-\dfrac{1}{2}g{{t}^{2}}$ --(3)
Now, at the topmost point ${{v}_{y}}=0$ but ${{v}_{x}}$ (initial velocity in the horizontal direction remains the same). This is because there is no acceleration of the projectile in the horizontal direction.
Therefore, the speed of the body at the topmost point is only the horizontal component ${{v}_{x}}=v\sin \theta $ (from the geometry of the figure).
The kinetic energy of a body $KE$ of mass $m$ moving at speed $v$ is given by
$KE=\dfrac{1}{2}m{{v}^{2}}$ --(4)
The potential energy $PE$ of a body of mass $m$ at a height $h$ above some reference point is given as
$PE=mgh$ --(5)
Now, for the motion of the projectile, the sum of its potential energy and kinetic energy remains constant as the total mechanical energy is conserved.
Therefore, the sum of its initial potential and kinetic energy will be the same as the sum of its final kinetic and potential energy.
If we consider the initial position of the projectile as the reference point, the height of the projectile at the topmost point will be nothing but $H$.
$\therefore \dfrac{1}{2}m{{v}^{2}}+mg\left( 0 \right)=\dfrac{1}{2}m{{v}_{x}}^{2}+mgH$ [Using (4) and (5)]
Where $m$ is the mass of the projectile.
$\therefore \dfrac{1}{2}{{v}^{2}}+0=\dfrac{1}{2}{{\left( v\sin \theta \right)}^{2}}+gH$ $\left( \because {{v}_{x}}=v\sin \theta \right)$
$\therefore \dfrac{1}{2}{{v}^{2}}=\dfrac{1}{2}{{v}^{2}}{{\sin }^{2}}\theta +gH$
$\therefore \dfrac{1}{2}{{v}^{2}}\left( 1-{{\sin }^{2}}\theta \right)=\dfrac{1}{2}{{v}^{2}}{{\cos }^{2}}\theta =gH$ $\left( \because 1-{{\sin }^{2}}\theta ={{\cos }^{2}}\theta \right)$
$\therefore H=\dfrac{{{v}^{2}}{{\cos }^{2}}\theta }{2g}$ --(6)
Using (6) in (3), we get
$\dfrac{{{v}^{2}}{{\cos }^{2}}\theta }{2g}=v\cos \theta t-\dfrac{1}{2}g{{t}^{2}}$
$\therefore \dfrac{1}{2}g{{t}^{2}}-v\cos \theta t+\dfrac{{{v}^{2}}{{\cos }^{2}}\theta }{2g}=0$
Now,
$t=\dfrac{-\left( -v\cos \theta \right)\pm \sqrt{{{\left( -v\cos \theta \right)}^{2}}-4\left( \dfrac{1}{2}g \right)\left( \dfrac{{{v}^{2}}{{\cos }^{2}}\theta }{2g} \right)}}{2\left( \dfrac{1}{2}g \right)}$ $\left( \because \text{For }a{{x}^{2}}+bx+c=0,\text{ }x=\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a} \right)$
$\therefore t=\dfrac{v\cos \theta \pm \sqrt{{{v}^{2}}{{\cos }^{2}}\theta -{{v}^{2}}{{\cos }^{2}}\theta }}{g}=\dfrac{v\cos \theta \pm \sqrt{0}}{g}=\dfrac{v\cos \theta \pm 0}{g}=\dfrac{v\cos \theta }{g}$ --(7)
Now, as explained earlier, the total time of flight will be twice of the time required to reach the topmost point.
Therefore, the total time of flight is
$T=2t=2\times \dfrac{v\cos \theta }{g}=\dfrac{2v\cos \theta }{g}$ --(8)
Again using (6), we get
$\therefore H=\dfrac{{{v}^{2}}{{\cos }^{2}}\theta }{2g}$
$2gH={{\left( v\cos \theta \right)}^{2}}$
Square rooting both sides we get
$\sqrt{2gH}=\sqrt{{{\left( v\cos \theta \right)}^{2}}}=v\cos \theta $--(9)
Putting (9) in (8), we get
$T=\dfrac{2}{g}\times \sqrt{2gH}=\sqrt{\dfrac{{{2}^{2}}\times 2gH}{{{g}^{2}}}}=\sqrt{\dfrac{8H}{g}}$
Hence, we have got the required expression for the time of flight.

So, the correct answer is “Option D”.

Note: This problem could also have been solved by using the direct formula for the time of flight of a body in terms of its maximum height reached in the projectile motion. However, we did not resort to the direct formula and instead resorted to deriving the same because it is always better to derive a formula than to memorize it unnecessarily and have a chance of writing the wrong formula during an exam. By deriving their minimum chance that we could go wrong with the formula.