Question

A projectile has a range of $40\;m$ and reaches a maximum height of $10\;m$. Find the angle at which the projectile is fired.

Answer 1

Hint: Obtain an expression for the range of a projectile, and then for the maximum height reached by the projectile. Divide the two equations and substitute the above mentioned values and solve arithmetically to arrive at the appropriate solution for the launch angle. Remember that the horizontal range is concerned with the x-axis whereas the maximum height is along the vertical y-axis, and the acceleration due to gravity is subject to change only during the vertical motion while it remains constant throughout the horizontal component of the projectile’s trajectory.

Formula Used:
Range $R = \dfrac{u^2 sin2\theta}{g}$
Maximum height $H = \dfrac{u^2sin^2\theta}{2g}$

Complete Solution:
Consider a projectile that is projected at an angle $\theta$ with respect to the x-axis, with an initial launch velocity u.

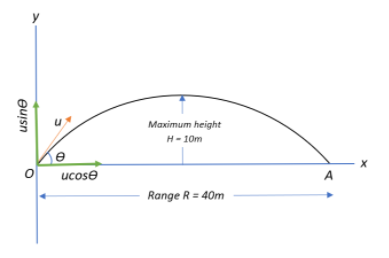
Let us first obtain an expression to find the Range of the projectile.
We can resolve the launch velocity into its horizontal and vertical components as:
$u_x = ucos\theta$ and $u_{y} = usin\theta$

The projectile experiences an acceleration due to gravity vertically downwards, therefore, we have:
$a_x=0$ and $a_y =-g$

Since projectile motion is two dimensional, the displacement of the projectile in horizontal and vertical directions in time t can be given by the kinematic equation of motion(s):
$s_x = u_x t + \dfrac{1}{2}a_xt^2 = ucos\theta.t$, and
$s_y = u_y t + \dfrac{1}{2}a_yt^2 = usin\theta.t -\dfrac{1}{2}gt^2$

Now, we know that, since the particle returns back to the ground at A, the vertical displacement of the particle will be $s_y=0$
$\Rightarrow 0 = usin\theta.t -\dfrac{1}{2}gt^2 \Rightarrow (t)(usin\theta - \dfrac{1}{2}gt) = 0$
This means that either $t=0$ or $t= \dfrac{2usin\theta}{g}$ .

We know that the projectile travels a finite horizontal distance $s_x$, so the correct choice would be $t= \dfrac{2usin\theta}{g}$, since $t=0$ signifies the initial time.

Substituting the value of t in the expression for $s_x$ we get:
$s_x = ucos\theta .t = ucos\theta.\left(\dfrac{2usin\theta}{g}\right) = \dfrac{u^2 2cos\theta sin\theta}{g}$
We use the trigonometric relation $2cos\theta sin\theta = sin2\theta$ and we get:
Range $R = s_x = \dfrac{u^2sin2\theta}{g}$

Let us now obtain an expression for the Maximum height of the projectile.
We begin by finding the time of ascent, t_a. Since the maximum height is the point at which the velocity of the projectile will be zero, we assume $v_y=0$ at this point. We also have initial vertical velocity $u_y = usin\theta$.

Using the equation of motion $v_y = u_y -gt_a$ for the ascent, we get:
$0 = usin\theta -gt_a \Rightarrow t_a = \dfrac{usin\theta}{g}$

From the previous Range derivation, we have an equation of motion for distance travelled by the projectile in the vertical direction given by
$s_y = usin\theta.t -\dfrac{1}{2}gt^2$. Substituting for $t=t_a$, and $s_y= s_{ymax} = H$ we get:
$H = usin\theta\left(\dfrac{usin\theta}{g}\right) - \dfrac{1}{2}g\left(\dfrac{usin\theta}{g}\right)^2$
$\Rightarrow H = \dfrac{u^2sin^2\theta}{g} - \dfrac{u^2sin^2\theta}{2g} = \dfrac{2u^2sin^2\theta-u^sin^2\theta}{2g}$
Maximum Height $H = \dfrac{u^2sin^2\theta}{2g} $

From the question, we have:
Range $R = 40 = \dfrac{u^2sin2\theta}{g} $ and $H = 10 = \dfrac{u^2sin^2\theta}{2g} $.

Dividing the above two equations, we get:
$\dfrac{40}{10} = \dfrac{\left(\dfrac{u^2sin2\theta}{g} \right)}{\left(\dfrac{u^2sin^2\theta}{2g} \right)}$
$\Rightarrow \dfrac{2sin2\theta}{sin^2\theta} = 4 \Rightarrow \dfrac{4sin\theta cos\theta}{sin^2\theta} = 4$
(since $sin2\theta = 2sin\theta cos\theta$)
$\Rightarrow \dfrac{cos\theta}{sin\theta} =1 \Rightarrow cot\theta=1 \Rightarrow \theta=cot^{-1}(1) = 45^{\circ}$

Therefore, the projectile is fired at an angle of $45^{\circ}$.

Note:
While resolving the vectors into their horizontal and vertical components, remember to assign the sine and cosine values correctly since it is a common misconception that the horizontal side is always the cosine part and the vertical side is the sine part.
The correct way to go about this would be to establish that the component that is adjacent to $\theta$ assumes a cosine value, whereas the component that is opposite to $\theta$ assumes a sine value.
Also, remember that during the ascent, since the projectile travels against the acceleration due to gravity, it assumes a negative sign, which is evident in our equations of motion that we defined in the problem. At maximum height, the velocity of the projectile will be zero, following which it begins its descent under the action of acceleration due to gravity.