Question

A positive charge $q$ of mass $m$ is moving along the positive x-axis. We wish to apply a uniform magnetic field $B$ for time $\Delta t$, so that the charge reverses its direction, crossing the y-axis at a distance of $d$. Then,
$\begin{align}
  & A)B=\dfrac{mv}{qd};\Delta t=\dfrac{\pi d}{v} \\
 & B)B=\dfrac{mv}{2qd};\Delta t=\dfrac{\pi d}{2v} \\
 & C)B=\dfrac{2mv}{qd};\Delta t=\dfrac{\pi d}{2v} \\
 & D)B=\dfrac{2mv}{qd};\Delta t=\dfrac{\pi d}{v} \\
\end{align}$

Answer 1

Hint: The velocity of the moving charge is assumed to be $v$. When a magnetic field is applied in a direction perpendicular to the moving charge, the charge reverses its direction and moves in the form of a circle, whose diameter is equal to the given distance $d$ in the y-axis. Since the charge moves in a circular path, centripetal force on the moving charge can be equated to the magnetic force acting on the moving charge. Time taken by the charge to reach the y-axis is derived from the distance travelled by the charge and the assumed velocity of the charge. Distance travelled by the charge to reach the y-axis is nothing but the circumference of the semicircular trajectory of motion of the charge.

Formula used:
$1){{F}_{C}}=\dfrac{m{{v}^{2}}}{r}$
$2){{F}_{B}}=qvB$
\[3){{F}_{C}}={{F}_{B}}\]
$4)\Delta t=\dfrac{D}{v}$

Complete answer:
We are provided with a positive charge $q$ of mass $m$, moving along the positive x-axis, as shown in the following figure. A uniform magnetic field $B$ for time $\Delta t$ is applied perpendicular to the moving charge into the plane of paper, so that the charge reverses its direction, crossing the y-axis at a distance $d$, as shown. We are required to determine the strength of the magnetic field as well as the time taken for the moving charge to reach the y-axis.

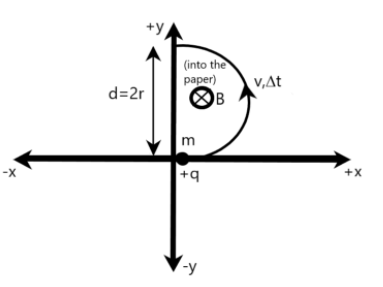
Firstly, let us assume that the charge is moving with a velocity $v$. From the figure, it is clear that the moving charge takes a circular path, while changing the direction when a uniform magnetic field is applied perpendicular to it. The given distance $d$ at which the moving charge touches the y-axis is nothing but the diameter of the circular trajectory of the moving charge. Clearly, radius of the circular path is given by
$r=\dfrac{d}{2}$
where
$r$ is the radius of the circular path
$d$ is the given distance at which the moving charge touches the y-axis, which is also equal to the diameter of the circular path
Let this be equation 1.
Since the charge is moving in a circular path, we know that centripetal force acts on the charge, which is given by
${{F}_{C}}=\dfrac{m{{v}^{2}}}{r}=\dfrac{m{{v}^{2}}}{\left( \dfrac{d}{2} \right)}=\dfrac{2m{{v}^{2}}}{d}$
where
${{F}_{C}}$ is the centripetal force acting on the moving charge
$m$ is the given mass of moving charge
$v$ is the assumed velocity of moving charge
$r=\dfrac{d}{2}$, from equation 1, is the radius of the circular path
Let this be equation 2.
Now, if ${{F}_{B}}$ represents the magnetic force acting on the moving charge, then, we know that ${{F}_{B}}$ is given by
${{F}_{B}}=qvB$
where
${{F}_{B}}$ is the magnetic force acting on the moving charge
$q$ is the moving charge
$v$ is the assumed velocity of moving charge
$B$ is the strength of magnetic field acting on the moving charge
Let this be equation 3.
Here, equation 2 and equation 3 can be equated because both these forces are equal and opposite to each other, which keep the moving charge stable and rotating.
Therefore, on equating equation 2 and equation 3, we have
\[{{F}_{C}}={{F}_{B}}\Rightarrow \dfrac{2m{{v}^{2}}}{d}=qvB\Rightarrow B=\dfrac{2m{{v}^{2}}}{qvd}=\dfrac{2mv}{qd}\]
Let this be equation 4.
Now, we also know that time taken by the moving charge to touch the y-axis is equal to the ratio of distance travelled by the moving charge to reach the y-axis and the velocity of the moving charge. Mathematically, time taken is given by
$\Delta t=\dfrac{D}{v}$
where
$\Delta t$ is the time taken by the moving charge to reach the y-axis
$D$ is the distance travelled by the moving charge to reach the y-axis
$v$ is the assumed velocity of the moving charge
Let this be equation 5.
Here, from the figure, it is clear that distance travelled by the moving charge to reach the y-axis while reversing its direction on the application of a magnetic field perpendicular to it, is given by
$D=\dfrac{2\pi r}{2}=\pi r=\pi \left( \dfrac{d}{2} \right)=\dfrac{\pi d}{2}$
where
$\dfrac{2\pi r}{2}$ is the circumference of semicircular trajectory of the moving charge
$r=\dfrac{d}{2}$, from equation 1, is the radius of the semicircular trajectory
$d$ is the diameter of the semicircular trajectory or the given distance at which the moving charge touches the y-axis
Let this be equation 6.
Substituting equation 6 in equation 5, we have
$\Delta t=\dfrac{D}{v}=\dfrac{\left( \dfrac{\pi d}{2} \right)}{v}=\dfrac{\pi d}{2v}$
Let this be equation 7.
Therefore, from equation 4 and equation 7, we can conclude that the strength of magnetic field $(B)$as well as the time taken $\left( \Delta t \right)$for the moving charge to reach the y-axis are $\dfrac{2mv}{qd}$ and $\dfrac{\pi d}{2v}$, respectively.

Hence, the correct answer is option $C$.

Note:
To solve this question, students need to assume the velocity of the moving charge as well as the direction of uniform magnetic field which is being applied to the moving charge. In the question, it is only given that the moving charge reverses its direction on the application of a uniform magnetic field. From this statement, we should understand that the magnetic field is applied perpendicular to the motion of charge, into the paper, for the moving charge to take a circular path and touch the y-axis, at a certain distance $d$.