Question

A polaroid making an angle 60° with electric vector then intensity reduced by a factor of:-
A.$\dfrac {1}{4}$
B.$\dfrac {3}{4}$
C.$\dfrac {1}{2}$
D.$\dfrac {1}{3}$

Answer 1

Hint: To solve this problem, use the equation for Malus’s law. It states that when completely plane polarized light incidents on an analyzer, the intensity of the light transmitted by the analyzer is directly proportional to the square of the cosine of angle between transmission axes of polarizer and analyzer. Substitute the value in the equation and find the factor by which intensity decreases.
Formula used:
$I ={I}_{0} {\cos}^{2}{\theta}$

Complete answer:

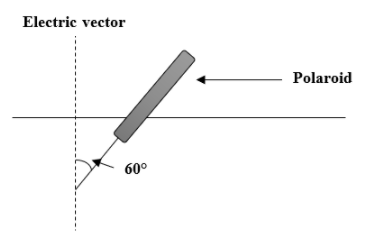
Given: $\theta$ = 60°
Malus’s law is given by,
$I ={I}_{0} {\cos}^{2}{\theta}$
Where, I is the intensity after polarization
            ${I}_{0}$ is the initial intensity
Substituting the value in above equation we get,
$I ={I}_{0}\times {\cos}^{2}{60°}$
$\Rightarrow I ={I}_{0}\times \dfrac {1}{4}$
$\Rightarrow \dfrac {I}{{I}_{0}}= \dfrac {1}{4}$
Hence, the intensity is reduced by a factor of $\dfrac {1}{4}$.

So, the correct answer is option A i.e. $\dfrac {1}{4}$.

Additional Information:
Polaroids are the materials used to restrict vibrations of waves from many planes to a single plane. The unpolarized lights are not confined to any particular plane, So, to restrict these vibrations to a single plane polaroid are used. It passes only the waves which vibrate in a single plane.

Note:
If the $\theta$= 0 or 180°, then $I = {I}_{0}$. That is the intensity of transmitted light is maximum when transmission axes of analyzer and polarizer are parallel to each other. Initial intensity and initial after polarization remain the same.
If the $\theta$= 90°, then $I = 0$. That is the intensity of transmitted light is minimum when transmission axes of analyzer and polarizer are perpendicular to each other. The intensity of light after polarization becomes zero.