Question

A point charge Q lies on the perpendicular bisector of an electric dipole of dipole p. If the distance of Q from the dipole is r (much larger than the size of the dipole), then the electric field at \[\theta \] is proportional to:
A. \[{P^2}\] and \[{r^{ - 3}}\]
B. \[{P^2}\] and \[{r^{ - 2}}\]
C. \[{P^{ - 1}}\] and \[{r^{ - 3}}\]
D. \[P\] and \[{r^{ - 3}}\]

Answer 1

Hint: Express the electric field at point charge Q. It will have only a horizontal component of electric field. In the expression, neglect the higher term of dipole distance. Use the expression for dipole moment , \[p = qa\], where, q is the charge and a is the dipole distance.

Formula used:
The electric field at a distance r from the point charge q is expressed as,
\[E = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{q}{{{r^2}}}\]
Here, \[{\varepsilon _0}\] is the permittivity of the free space.

Complete step by step answer:
We have given that the point charge Q lies on the perpendicular bisector and the distance between the point charge Q and dipole is much larger than the size of the dipole as shown in the figure below.

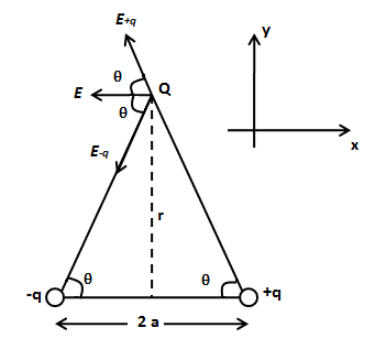
In the above figure, \[{E_{ - q}}\] is the electric field due to charge \[ - q\] and \[{E_{ + q}}\] is the electric field due to charge \[ + q\]. The vertical component of \[{E_{ - q}}\] is along the negative y-axis and vertical component of \[{E_{ + q}}\] is along the positive y-axis. Hence we can say they cancel out. Now, the net electric field of the dipole at point charge Q is due the horizontal components of \[{E_{ + q}}\] and \[{E_{ - q}}\]. Therefore, we see that the electric field at \[\theta \] is the sum of horizontal components of \[{E_{ + q}}\] and \[{E_{ - q}}\].

We can express the magnitude of electric field at point charge Q due to charge \[ - q\] as follows,
\[\left| {{E_{ - q}}} \right| = k\dfrac{q}{{{r^2} + {a^2}}}\] …… (1)
Here, k is the constant and it has the value \[k = \dfrac{1}{{4\pi {\varepsilon _0}}}\].
We can express the magnitude of electric field at point charge Q due to charge \[ + q\] as follows,
\[\left| {{E_{ + q}}} \right| = k\dfrac{q}{{{r^2} + {a^2}}}\] …… (2)

Since the electric field at Q is the sum of horizontal components of electric field along the negative x-axis, we can write,
\[\vec E = \left| {{E_{ + q}}} \right|\cos \theta \left( { - \hat i} \right) + \left| {{E_{ - q}}} \right|\cos \theta \left( { - \hat i} \right)\]
\[ \Rightarrow \vec E = k\dfrac{q}{{{r^2} + {a^2}}}\cos \theta \left( { - \hat i} \right) + k\dfrac{q}{{{r^2} + {a^2}}}\cos \theta \left( { - \hat i} \right)\]
\[ \Rightarrow \vec E = k\dfrac{{2q}}{{{r^2} + {a^2}}}\cos \theta \left( { - \hat i} \right)\] …… (3)
From the trigonometry of the above figure, we can express the \[\cos \theta \] as follows,
\[\cos \theta = \dfrac{a}{{\sqrt {{r^2} + {a^2}} }}\]
Therefore, we can rewrite equation (3) as,
\[\vec E = k\left( {\dfrac{{2q}}{{{r^2} + {a^2}}}} \right)\left( {\dfrac{a}{{\sqrt {{r^2} + {a^2}} }}} \right)\left( { - \hat i} \right)\]
\[ \Rightarrow \vec E = k\dfrac{{2qa}}{{{{\left( {{r^2} + {a^2}} \right)}^{3/2}}}}\left( { - \hat i} \right)\]
But we know that the dipole moment of an electric dipole is expressed as,
\[\hat P = qa\,\hat i\]
Therefore, the above equation becomes,
\[\vec E = - k\dfrac{{2P}}{{{{\left( {{r^2} + {a^2}} \right)}^{3/2}}}}\]
Now, we have given that the distance h is very much larger than the distance a. Therefore, we can neglect the term \[{a^2}\] in the denominator.
\[\vec E = - k\dfrac{{2P}}{{{{\left( {{r^2}} \right)}^{3/2}}}}\]
\[ \therefore \vec E = - k\dfrac{{2P}}{{{r^3}}}\]
Thus, from the above equation, we can infer that the electric field is proportional to P and \[{r^{ - 3}}\].

So, the correct answer is option D.

Note: Remember, dipole moment is a vector quantity which directs from negative charge to positive charge along the dipole. In our solution, since the dipole is along the positive x-axis, we have expressed it as \[\hat P = qa\,\hat i\]. If the negative charge is on the right side and positive on the left, we would have \[\hat P = qa\left( { - \,\hat i} \right)\].