Question

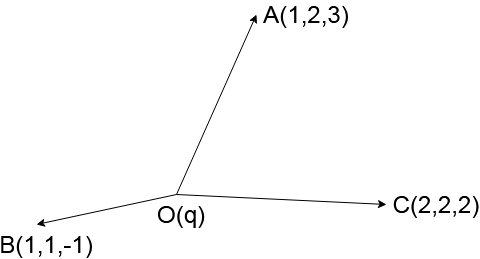
A point charge \[q\] is placed at origin. Let ${\vec E_A}$ , ${\vec E_B}$ and ${\vec E_C}$ be the electric field at three points $A(1,2,3)$, $B(1,1, - 1)$ and $C(2,2,2)$ due to charge \[q\] . Consider the following statement and choose the correct alternative.
(i). ${\vec E_A} \bot {\vec E_B}$
(ii). $|{\vec E_B}| = 4|{\vec E_C}|$
(a). Only [i] is correct
(b). Only [ii] is correct
(c). Both [i] and [ii] is correct
(d). Both [i] and [ii] are wrong

Answer 1

- Hint: You can start by defining coulomb’s force and electric field. Then use the equation $\vec E = \dfrac{{Kq}}{{|\vec r{|^2}}} \times \dfrac{{{{\vec r}_{}}}}{{|r|}}$ to find the electric field at points \[A\] , \[B\] and \[C\] . Then find out if \[{\vec E_A} \bot {\vec E_B}\] by calculating if \[{\vec E_A}.{\vec E_B} = 0\] . Then compare the values of $|{\vec E_B}|$ and \[|{\vec E_C}|\] to find out if $|{\vec E_B}| = 4|{\vec E_C}|$. Use this method to reach the solution.

Complete step-by-step answer:
The force that a charge experiences in the presence of another charge is known as electrostatic force. This force is also known as Coulomb force, after the name of its discoverer Charles-Augustin de Coulomb.
The charge experiences Coulomb’s force due to the formation of an electric field around the other charge. Imagine a fisherman entrapping a fish in its net and pulling it, this is somewhat how electric fields trap a charge.

The electric field at any point is given by
$\vec E = \dfrac{{Kq}}{{|\vec r{|^2}}} \times \dfrac{{{{\vec r}_{}}}}{{|r|}}$
The electric field on point $A$ is
${\vec E_A} = \dfrac{{Kq}}{{|{{\vec r}_{OA}}{|^2}}} \times \dfrac{{{{\vec r}_{OA}}}}{{|{r_{OA}}|}}$
$ \Rightarrow {\vec E_A} = \dfrac{{Kq}}{{{{(\sqrt {14} )}^2}}} \times \dfrac{{(\hat i + 2\hat j + 3\hat k)}}{{\sqrt {14} }}$
$ \Rightarrow {\vec E_A} = \dfrac{{Kq(\hat i + 2\hat j + 3\hat k)}}{{14\sqrt {14} }}$
The electric field at point $B$ is
${\vec E_B} = \dfrac{{Kq}}{{|{{\vec r}_{OB}}{|^2}}} \times \dfrac{{{{\vec r}_{OB}}}}{{|{r_{OB}}|}}$

$ \Rightarrow {\vec E_B} = \dfrac{{Kq}}{{{{(\sqrt 3 )}^2}}} \times \dfrac{{(\hat i + \hat j - \hat k)}}{{\sqrt 3 }}$
$ \Rightarrow {\vec E_B} = \dfrac{{Kq(\hat i + \hat j - \hat k)}}{{3\sqrt 3 }}$
The electric field at point $C$ is
${\vec E_C} = \dfrac{{Kq}}{{|{{\vec r}_{OC}}{|^2}}} \times \dfrac{{{{\vec r}_{OC}}}}{{|{r_{OC}}|}}$
$ \Rightarrow {\vec E_C} = \dfrac{{Kq}}{{{{(\sqrt {12} )}^2}}} \times \dfrac{{(2\hat i + 2\hat j + 2\hat k)}}{{\sqrt {12} }}$
$ \Rightarrow {\vec E_C} = \dfrac{{Kq(\hat i + \hat j + \hat k)}}{{12\sqrt 3 }}$
Let’s find out what the value of ${\vec E_A}.{\vec E_B}$ is
\[{\vec E_A}.{\vec E_B} = \left( {\dfrac{{Kq}}{{14\sqrt {14} }}} \right)\left( {\dfrac{{Kq}}{{3\sqrt 3 }}} \right)(1\hat i + 2\hat j + 3\hat k)(\hat i + \hat j - \hat k)\]
\[ \Rightarrow {\vec E_A}.{\vec E_B} = \left( {\dfrac{{Kq}}{{3\sqrt 3 }}} \right)\left( {\dfrac{{Kq}}{{12\sqrt 3 }}} \right)(1 + 2 - 3)\]
\[ \Rightarrow {\vec E_A}.{\vec E_B} = 0\]
\[\because {\vec E_A}.{\vec E_B} = 0\]
\[\therefore {\vec E_A} \bot {\vec E_B}\]
The magnitude of electric field at point \[A\] and point \[B\] are
\[|{\vec E_B}| = \dfrac{{Kq}}{{3\sqrt 3 }}\] (Equation 1)
And \[|{\vec E_C}| = \dfrac{{Kq}}{{12\sqrt 3 }}\] (Equation 2)
Dividing equation 1 by equation 2, we get
\[\dfrac{{|{{\vec E}_B}|}}{{|{{\vec E}_C}|}} = \dfrac{{\dfrac{{Kq}}{{3\sqrt 3 }}}}{{\dfrac{{Kq}}{{12\sqrt 3 }}}}\]
\[\dfrac{{|{{\vec E}_B}|}}{{|{{\vec E}_C}|}} = 4\]
\[|{\vec E_B}| = 4|{\vec E_C}|\]
As we can see that both options i and ii are correct.
Hence, option (c). is the correct choice.

Note: In this type of problem, we view the electric field as a vector quantity. A vector quantity is a quantity that has both a magnitude and a direction. In most of the problems concerning the electric field, we mostly deal with the magnitude of the electric field, but in questions such as these we have to consider the direction of the electric field in all 3-dimensions and use the related equations i.e. $\vec E = \dfrac{{Kq}}{{|\vec r{|^2}}} \times \dfrac{{{{\vec r}_{}}}}{{|r|}}$.