Question

A point charge +Q is positioned at the center of the base of a square pyramid as shown in the figure. What is the electric flux through one of the four identical upper faces of the pyramid?
                       

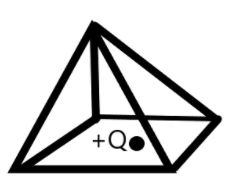
Answer 1

Hint: We need to understand the relation between the charge placed in a system, the orientation of the system and the electric flux passing through a plane. We can use the Gauss’ law in electrostatics to find the solution for the magnitude of flux.

Complete answer:
The electric charges are the primary sources of the electric field. We know from the basic electrostatics that a positive point charge has an electric field emerging from the charge and going out to infinity and a negative charge has an incoming direction for the electric field.
The strength of the electric field is dependent on the magnitude of charge possessed by the charge and inversely proportional to the distance from the charge to the point where the electric field is being calculated.
The electric flux is defined as the electric field through a plane surface equidistant from the point charge. If we consider a point charge, then the equidistant points join together to form a spherical surface. So, the electric flux can be mathematically given from the gauss’ law as –
\[\begin{align}
  & \phi =\int{{}}E.dA \\
 & \Rightarrow \phi =\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{q}{{{r}^{2}}}4\pi {{r}^{2}} \\
 & \Rightarrow \phi =\dfrac{q}{{{\varepsilon }_{0}}} \\
\end{align}\]
                                   

So, in the present situation the electric flux emerging from the point charge can be given as –
\[\phi =+\dfrac{Q}{{{\varepsilon }_{0}}}\]
We know that we need to find the flux through one of the identical faces of the square pyramid. Since the flux can be considered only in the upward direction, the flux that passes through the pyramid reduces to –
\[\phi =+\dfrac{Q}{2{{\varepsilon }_{0}}}\]
Now, when we consider one face of the pyramid, the flux again reduces by one-fourth of the above value. So, the electric flux through one of the faces of the pyramid becomes –
\[\begin{align}
  & \phi =\dfrac{1}{4}\dfrac{Q}{2{{\varepsilon }_{0}}} \\
 & \therefore \phi =\dfrac{Q}{8{{\varepsilon }_{0}}} \\
\end{align}\]
The flux through one of the four identical faces of the square pyramid is \[\dfrac{Q}{8{{\varepsilon }_{0}}}\].
This is the required solution.

Note:
The electric flux turns out to be a scalar quantity as its direction is insignificant. Also, it is the dot product of the electric field and the area element of the surface. The positive charges have flux going out of the surface and the reverse for the negative charges.