Question

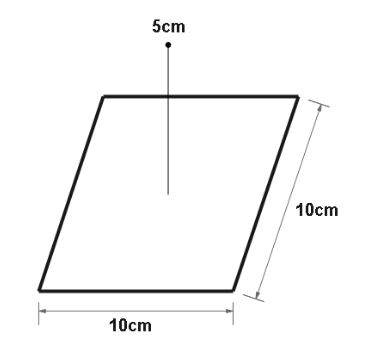
A point charge \[ + 10\mu C\] is a distance $5\,cm$ directly above the centre of a square of side $10\,cm$ , as shown. What is the magnitude of the electric flux through the square? (Hint: Think of the square as one face of a cube with an edge $10\,cm$ .)

Answer 1

Hint: To solve this question, one must know about the flux and Gauss’s law here. In this solution, we'll use the formula of Gauss's law to calculate the flux through the surface we've been provided. The surface represents one of the cube's sides through which the flux will flow and hence we got our required solution.

Formula used:
$\phi = \dfrac{q}{{{\varepsilon _0}}}$
Where, $\phi $ is the flux and $q$ is the charge.

Complete step by step answer:
According to the question, we have a charge \[ + 10\mu C\]. And we can calculate the flux from the given charge by the help of Gauss’s law,
$\phi = \dfrac{q}{{{\varepsilon _0}}}$
This flux will now be emitted in all directions at the same time. To find the flux through the given surface, imagine the charge is enclosed by a cube with a side of 10 cm. The flux through the cube will then be as follows:
$\phi = \dfrac{q}{{{\varepsilon _0}}}$

Because the flux is distributed evenly, the flux through one surface will be 1/6th of the total flux, because the cube has six sides. Therefore, the flux through the one surface is given by,
$\phi = \dfrac{q}{{6{\varepsilon _0}}}$
Now, substituting all the given values in above equation,
\[q = 10\mu C = 10 \times {10^{ - 6}}C \\
\Rightarrow {\varepsilon _0} = 8.85 \times {10^{ - 12}} \\ \]
$\Rightarrow \phi = \dfrac{{10 \times {{10}^{ - 6}}}}{{6 \times 8.85 \times {{10}^{ - 12}}}} \\
\Rightarrow \phi = \dfrac{{10 \times {{10}^{ - 6}}}}{{53.1 \times {{10}^{ - 12}}}} \\
\therefore \phi = 1.88 \times {10^5}N{m^2}{\text{ }}{C^{ - 1}} \\ $

Therefore, the magnitude of the electric flux through the square is $1.88 \times {10^5}N{m^2}{\text{ }}{C^{ - 1}}$.

Note: The charge must be near the centre of the cube if the flux surface is to be considered a cube. In this scenario, the charge is 5 centimetres away from one of the cube's surfaces, which is also where the cube's centre is located. Gauss's law allows us to directly compute the flux through the surface as 1/6th of the total flux using this symmetry.