Question

A point \[A\left( p,q \right)\] is 2 units away from x-axis and 5 units from y-axis and it lies in \[{{2}^{nd}}\] quadrant. Find \[\left( -\left( p+q \right) \right)\]

Answer 1

Hint: If the point given is x units away from y-axis, then its x-coordinate value will be x and if it is y units away from y-axis, then its y-coordinate value will be y. As the point lies in \[{{2}^{nd}}\] quadrant the point should have negative x-coordinate and positive y-coordinate.

Complete step-by-step answer:
In the question, we are told that, a point A lies in the second quadrant with a given condition that it is 2 units away from the x-axis and 5 units away from the y-axis. It is also said that, if the point A is represented as (p, q) then, we have to find the value of \[\left( -\left( p+q \right) \right)\]
First, let’s see the given features of point A which is said to lie in the second quadrant, which means it’s x-coordinate will be positive.
Now, we were given that, the point is 2 units away from x-axis, then the only possibility is that the point will be above x-axis, thus, we can say that the y-coordinate will be 2. It is also said that the mentioned point is away by 5 units from the y-axis as it is located in 2 quadrants. Thus, we can say the point is left to the y-axis by 5 units, thus, its x-coordinate will be -5.
Now, as the x-coordinate is -5 and y-coordinate is 2, thus, the point will be \[\left( -5,2 \right)\].
Thus, the point A’s coordinate is \[\left( -5,2 \right)\]. Hence, on comparing it with (p, q) we can say that the value of p is -5 and q is 2.
We have to find value of \[\left( -\left( p+q \right) \right)\] which on substituting it will be \[-5\left( -5+2 \right)\Rightarrow -\left( -3 \right)\Rightarrow 3\].

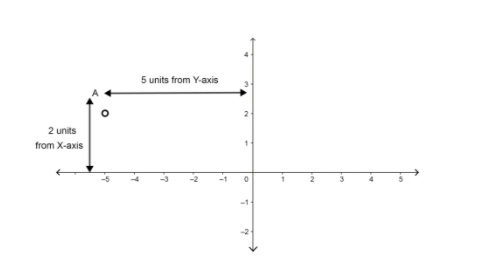
Note: Students generally confuse the answer \[\left( -5,2 \right)\] with \[\left( 2,-5 \right)\] and hence get the answer wrong. Hence, they can also see it graphically. We can represent it as,