Question

A Plano-convex lens fits exactly into a Plano-concave lens. Their plane surfaces are parallel to each other. If the lenses are made of different material of refractive indices ${{\mu }_{1}}$ and${{\mu }_{2}}$, and $R$ is the radius of curvature of the curved surface of the lenses, then focal length of combination is:
$\text{A}\text{. }\dfrac{R}{{{\mu }_{1}}-{{\mu }_{2}}}$
$\text{B}\text{. }\dfrac{2R}{{{\mu }_{2}}-{{\mu }_{1}}}$
$\text{C}\text{. }\dfrac{R}{2\left( {{\mu }_{1}}-{{\mu }_{2}} \right)}$
$\text{D}\text{. }\dfrac{R}{2-\left( {{\mu }_{1}}+{{\mu }_{2}} \right)}$

Answer 1

Hint: We will calculate the separate focal length of both the lenses using Lens maker formula. Then we will apply the Lens maker formula to the combination of both the lenses to obtain the final focal length of the combination. For Plano-convex and Plano-concave lenses , one of the radius of curvature is considered as infinity and the other radius of curvature is equal to the radius of the sphere of which the lens is a part of.

Formula used:
$\dfrac{1}{f}=\left( \mu -1 \right)\left( \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right)$

Complete step-by-step solution -
Optical lenses are described as the transmissive optical appliances that either focus or disperse the incident light beam by means of refraction. A simple optical lens is made of a single piece of transparent, or glass, material, while a compound lens consists of several simple lenses being arranged along a common axis.
Lens maker formula is the relation between the focal length of a lens to the refractive index of its material. Lens maker formula is basically used to construct a lens with the specified value of focal length. A lens consists of two curved surfaces, but these are not exactly the same in curvature or material. If we know the refractive index and the radius of curvature of both surfaces, then we can determine the focal length of the lens by using Lens maker formula.
Equation for Lens maker formula:
$\dfrac{1}{f}=\left( \mu -1 \right)\left( \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right)$
Where,
$f$ is the focal length of combination
$\mu $ is the refractive index of material of lens
${{R}_{1}}\text{ and }{{R}_{2}}$ are radius of curvature of both surfaces
Plano-convex lenses are the positive focal length elements that have one spherical surface and one flat surface.
Plano-concave lenses are optical lenses with one concave surface and one flat surface. They have negative focal length.
We are given that a Plano-convex lens fits exactly into a Plano-concave lens and their plane surfaces are parallel to each other. We have to calculate focal length of the combination of two lenses.

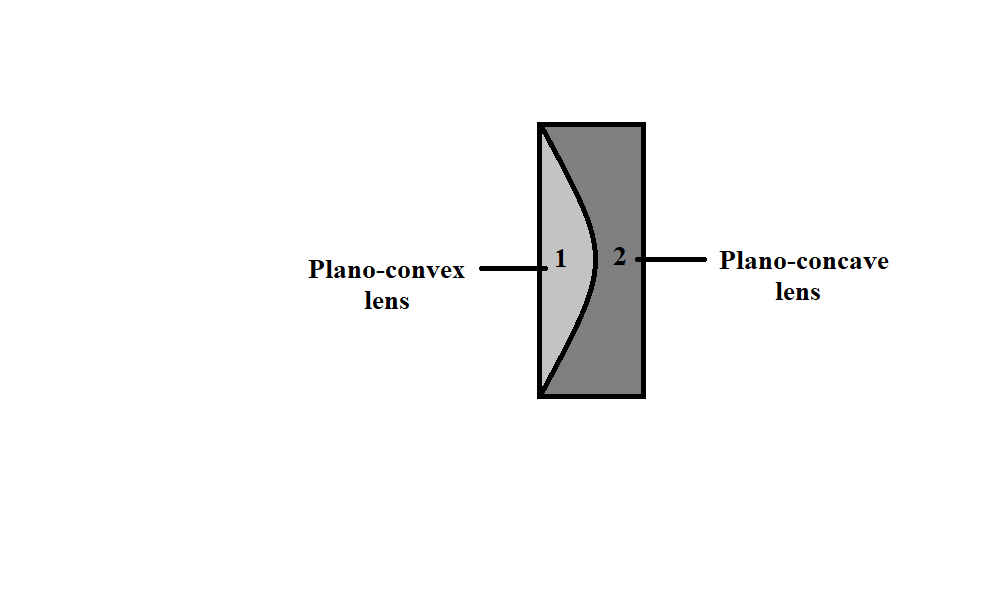
According to Lens maker formula, we have,
$\dfrac{1}{f}=\left( \mu -1 \right)\left( \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right)$
For Plano-convex lens,
$\begin{align}
  & {{R}_{1}}=\infty \\
 & {{R}_{2}}=-R \\
\end{align}$
Therefore,
\[\begin{align}
  & \dfrac{1}{{{f}_{1}}}=\left( {{\mu }_{1}}-1 \right)\left( \dfrac{1}{\infty }-\dfrac{1}{\left( -R \right)} \right) \\
 & \dfrac{1}{{{f}_{1}}}=\dfrac{{{\mu }_{1}}-1}{R} \\
\end{align}\]
For Plano-concave lens,
$\begin{align}
  & {{R}_{1}}=-R \\
 & {{R}_{2}}=\infty \\
\end{align}$
Therefore,
\[\begin{align}
  & \dfrac{1}{{{f}_{2}}}=\left( {{\mu }_{2}}-1 \right)\left( \dfrac{1}{-R}-\dfrac{1}{\infty } \right) \\
 & \dfrac{1}{{{f}_{2}}}=\dfrac{1-{{\mu }_{2}}}{R} \\
\end{align}\]
Thus, focal length of the combination,
$\dfrac{1}{F}=\dfrac{1}{{{f}_{1}}}+\dfrac{1}{{{f}_{2}}}$
Putting the values,
`$\begin{align}
  & \dfrac{1}{F}=\dfrac{{{\mu }_{1}}-1}{R}+\dfrac{1-{{\mu }_{2}}}{R} \\
 & F=\dfrac{R}{{{\mu }_{1}}-{{\mu }_{2}}} \\
\end{align}$
Focal length of combination of Plano-convex lens and Plano-concave lens is$\dfrac{R}{{{\mu }_{1}}-{{\mu }_{2}}}$.
Hence, the correct option is A.

Note: Convex lens converges the incident beam of light; therefore, the rays converge at a point in front of the lens. So, image distance is taken as positive. Thus, focal length of a convex lens is considered as positive. In the case of a Concave lens, the focal length is considered as negative, and this is the distance to the point from which a collimated beam of light appears to be diverging after passing through the lens.