Question

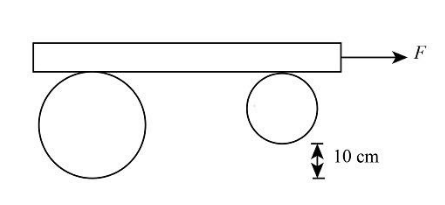
A plank of mass $102.5\;{\rm{kg}}$ is placed over two cylindrical radii $R = 10\;{\rm{cm}}$ and $r = 5\;{\rm{cm}}$. Mass of rollers is $20\;{\rm{kg}}$, respectively. Plank is pulled towards right by applying a horizontal force $F = 35\;{\rm{N}}$ as shown in fig. During the first second of motion the plank gets displaced by $10\;{\rm{cm}}$. If the plank remains horizontal and slipping does not take place, calculate the magnitude and direction of force of friction acting between Plank and bigger roller.

(A) $3\;{\rm{N}}$ towards left
(B) $1\;{\rm{N}}$ towards left
(C) $3\;{\rm{N}}$ towards right
(D) $1\;{\rm{N}}$ towards right

Answer 1

Hint: We can determine the frictional force between bigger roller and plank with the help of torque expression. First, draw the free body diagram of the bigger cylinder and determine the linear and angular acceleration of the roller and then use the torque expression for the determination of frictional force.

Complete step by step answer:
We know that the motion of the plank is in a forward direction. The frictional force on the plank acts opposite to the applied force, and the frictional force on the bigger roller acts in the opposite direction of the plank's frictional force. We will use this formation and draw the free body diagram of the bigger roller.

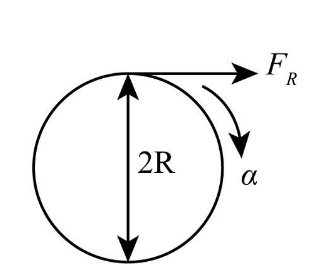
Write the equation of motion so that we can calculate the linear acceleration of the roller.
$s = ut + \dfrac{1}{2}a{t^2}$
Here $t$ is the time, $u$ is the roller's initial speed, $a$ is the linear acceleration and $s$ is displacement.
Substitute the given values in the above equation.
Therefore, we get
\[
\Rightarrow 10\;{\rm{cm \times }}\dfrac{{{\rm{1}}\;{\rm{m}}\;}}{{100\;{\rm{cm}}}} = (0) + \dfrac{1}{2}a{\left( {1\;{\rm{s}}} \right)^2}\\
\Rightarrow a = 2 \times 0.1\dfrac{{\rm{m}}}{{{s^2}}}\\
\Rightarrow a = 0.2\;{{\rm{m}} {\left/
{\vphantom {{\rm{m}} {{{\rm{s}}^{\rm{2}}}}}} \right.
} {{{\rm{s}}^{\rm{2}}}}}
\]
Now we will use the relation of linear and angular acceleration so that we will determine the tangential acceleration. Therefore, we get
$
\Rightarrow a = \alpha D\\
\Rightarrow a = \alpha \left( {2R} \right)
$
Here, $\alpha $ is the angular acceleration and $D$ is the diameter of the bigger roller, put $\Rightarrow a = 0.2\;{{\rm{m}} {\left/
{\vphantom {{\rm{m}} {{{\rm{s}}^{\rm{2}}}}}} \right.
} {{{\rm{s}}^{\rm{2}}}}}$ and $R = 10\;{\rm{cm}}$ in the above equation.
$
\Rightarrow 0.2\;{{\rm{m}} {\left/
{\vphantom {{\rm{m}} {{{\rm{s}}^{\rm{2}}}}}} \right.
} {{{\rm{s}}^{\rm{2}}}}} = \alpha \left( {2 \times 10\;{\rm{cm}} \times \dfrac{{1\;{\rm{m}}}}{{100\;{\rm{cm}}}}} \right)\\
\Rightarrow \alpha = \dfrac{{0.2\;{{\rm{m}} {\left/
{\vphantom {{\rm{m}} {{{\rm{s}}^{\rm{2}}}}}} \right.
} {{{\rm{s}}^{\rm{2}}}}}}}{{0.2\;{\rm{m}}}}\\
\Rightarrow \alpha = 1\;{\rm{rad/s}}
$
Write the expression of the torque acting on the roller.
$\Rightarrow T = {F_R} \times 2R$ …… (1)
Here, ${F_R}$ is the frictional force.
But we know that another expression of torque is,
$\Rightarrow T = I\alpha $ …… (2)
Here, $I$ is the rotational moment of inertia.
We know that the expression of the rotational moment of the inertia is,
$
\Rightarrow I = {I_{center}} + {I_{side}}\\
\Rightarrow I = \dfrac{{M{R^2}}}{2} + M{R^2}
$ …… (3)
Here , $M$ is the mass of the bigger roller, ${I_{center}}$ is the moment of inertia at the centre of the roller and ${I_{side}}$ is the momentum of inertia at the roller's circumference.
We will use equation (1), (2), and (3) for the calculation of the frictional force between the bigger roller and the plank.
Therefore, we get
$
\Rightarrow {F_R} \times 2R = I\alpha \\
\Rightarrow {F_R} \times 2R = \left( {\dfrac{{M{R^2}}}{2} + M{R^2}} \right)\alpha \\
\Rightarrow {F_R} \times 2R = \dfrac{{3M{R^2}}}{2}a\\
\Rightarrow {F_R} = \dfrac{{3MR}}{4}a
$
Substitute the values in the above equation.
\[
\Rightarrow {F_R} = \dfrac{{3MR}}{4}a\\
\Rightarrow {F_R} = \dfrac{{3 \times 40\;{\rm{kg}} \times \left( {10\;{\rm{cm}} \times \dfrac{{1\;{\rm{m}}}}{{100\;{\rm{cm}}}}} \right)}}{4}1\;{\rm{rad/s}}\\
\Rightarrow {F_R} = 3\;{\rm{kg}} \cdot {\rm{m}} \cdot {\rm{rad/s}}\\
\Rightarrow {{\rm{F}}_R} = 3\;{\rm{N}}
\]
Therefore, the frictional force magnitude is $3\;{\rm{N}}$, and its direction is towards the right because the magnitude of the friction is positive.

Note:Remember the relation between linear and angular acceleration as well as expressions of the torque. Also, perform the required unit conversion during the calculation like centimeter into the meter to obtain the correct answer present in the given options.