Question

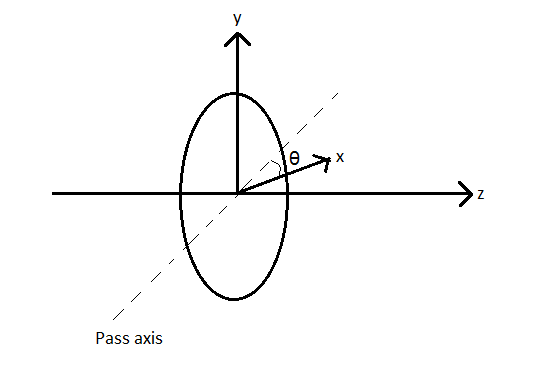
A plane polarized light is incident on a polarizer with its pass axis making angle $\theta $ with x-axis, as shown in the figure. At four different values of $\theta $, $\theta ={{8}^{0}},{{38}^{0}},{{188}^{0}},\text{ and }{{218}^{0}}$, the observed intensities are the same. What is the angle between the direction of polarization and the x-axis?

A) $\text{ }{{203}^{0}}$ B) $\text{ }{{45}^{0}}$ C) $\text{ }{{98}^{0}}$ D) $\text{ 12}{{\text{8}}^{0}$

Answer 1

Hint: This problem can be solved by using Mallus’ law which gives the relation between the emergent and initial intensity of light after passing thorugh a polarizer. By using the angle between a the pass axis of the polarizer and the light and plugging in the information given, we can get the answer.
Formula used:
$I={{I}_{0}}{{\cos }^{2}}\theta $

Complete step-by-step answer:
According to Mallus’ law the emergent intensity $I$ of plane-polarized light after passing through a polarizer is given by
$I={{I}_{0}}{{\cos }^{2}}\theta $ --(1)
Where ${{I}_{0}}$ is the intensity of the light before entering the polarizer and $\theta $ is the angle made by the direction of polarization of the light with the pass axis of the polarizer.

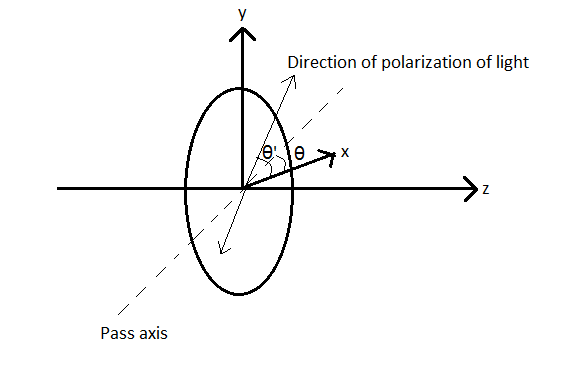
Let the direction of polarization of the light be such that it makes an angle $\theta '$ with the x-axis. Therefore, the angle made by the direction of polarization with the pass axis of the polarizer is $\theta '-\theta $.
Therefore, using (1), the intensity of the emergent light will be
$I={{I}_{0}}{{\cos }^{2}}\left( \theta '-\theta \right)$ --(2)
Where ${{I}_{0}}$ is the intensity of the light before entering the polarizer.
Now, according to the question,
When $\theta ={{8}^{0}},{{38}^{0}},{{188}^{0}},{{218}^{0}}$, the intensities are same.
Therefore, putting these values in (2), we get,
${{I}_{0}}{{\cos }^{2}}\left( \theta '-{{8}^{0}} \right)={{I}_{0}}{{\cos }^{2}}\left( \theta '-{{38}^{0}} \right)={{I}_{0}}{{\cos }^{2}}\left( \theta '-{{188}^{0}} \right)={{I}_{0}}{{\cos }^{2}}\left( \theta '-{{218}^{0}} \right)$ $\therefore {{\cos }^{2}}\left( \theta '-{{8}^{0}} \right)={{\cos }^{2}}\left( \theta '-{{38}^{0}} \right)={{\cos }^{2}}\left( \theta '-{{188}^{0}} \right)={{\cos }^{2}}\left( \theta '-{{218}^{0}} \right)$ --(3)
Now, putting the options one by one in (3), we get,
Putting option A) $\theta '={{203}^{0}}$
$\therefore {{\cos }^{2}}\left( {{203}^{0}}-{{8}^{0}} \right)={{\cos }^{2}}\left( {{203}^{0}}-{{38}^{0}} \right)={{\cos }^{2}}\left( {{203}^{0}}-{{188}^{0}} \right)={{\cos }^{2}}\left( {{203}^{0}}-{{218}^{0}} \right)$ $\therefore {{\cos }^{2}}\left( {{195}^{0}} \right)={{\cos }^{2}}\left( {{165}^{0}} \right)={{\cos }^{2}}\left( {{15}^{0}} \right)={{\cos }^{2}}\left( -{{15}^{0}} \right)$
Which is true since,
${{\cos }^{2}}\left( {{195}^{0}} \right)={{\cos }^{2}}\left( {{180}^{0}}+{{15}^{0}} \right)={{\left( -\cos {{15}^{0}} \right)}^{2}}={{\cos }^{2}}{{15}^{0}}$ $\left( \because \cos \left( {{180}^{0}}+\theta \right)=-\cos \theta \right)$ ${{\cos }^{2}}{{165}^{0}}={{\cos }^{2}}\left( {{180}^{0}}-{{15}^{0}} \right)={{\left( -\cos {{15}^{0}} \right)}^{2}}={{\cos }^{2}}{{15}^{0}}$ $\left( \because \cos \left( {{180}^{0}}-\theta \right)=-\cos \theta \right)$ ${{\cos }^{2}}\left( -{{15}^{0}} \right)={{\cos }^{2}}{{15}^{0}}$ $\left( \because \cos \left( -\theta \right)=\cos \theta \right)$
Hence, as option A) satisfies the conditions, therefore it is the correct option.
Note:
The final answer could also have been found out by writing and manipulating the trigonometric identities in (3). However, that would have taken a lot of time and unnecessary equations to find out the value of $\theta '$ with a chance of a lot of calculation mistakes and a lengthy process. It was much easier to just plug in the options and check the validity of the condition for the option. Sometimes, especially in competitive exams, it is better to find out a necessary condition that the answer must fulfill and go about plugging in the options in this condition to eliminate some of them and even find the answer at once.