Question

A plane banks its wings $30^\circ $ relative to the horizontal to enter into a circular turn. The circular path has a radius of 1500 m. Which of these values best represent the velocity of the plane if the lift force exerted on the wings is equal to twice the weight of the plane?
A. 120 m/s
B. 140 m/s
C. 160 m/s
D. 240 m/s
E. 320 m/s

Answer 1

Hint: We have to understand the definition of centripetal force for this question. A centripetal force is a force that makes a body follow a curved path. The direction is always orthogonal to the motion of the body and towards the fixed point of the instantaneous center of curvature of the path. It is basically the force that keeps the body moving around a fixed point.

Complete step by step answer:
In non-ideal cases, the circular motion of a body will not have constant angular velocity but it will slow down or pick up pace regularly. The total acceleration of a body moving in a circular motion is the resultant of two types of accelerations, namely Centripetal and Tangential acceleration.
$\overrightarrow a = {\overrightarrow a _c} + {\overrightarrow a _t}$
Let us consider a non-uniform circular motion as shown:

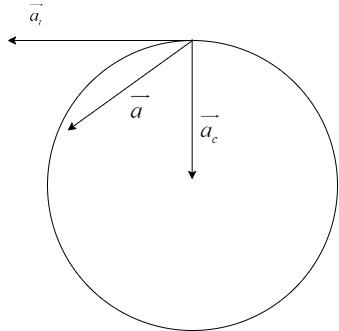
In a non-uniform circular motion, the body not only changes its angular velocity per unit time but also, the direction of the velocity vector. Since the velocity vector, which is a tangent to the direction of motion of the body, keeps changing every second, we get an additional component of acceleration. This component of acceleration is called Tangential acceleration.
Tangential acceleration, $\left| {{a_t}} \right| = r\alpha$
$\alpha$ is called the angular acceleration, which means the change in angular velocity in radians per second.
$\alpha = \dfrac{\omega }{t}$
There is one more component of acceleration, for the actual change in the velocity per unit time and is directed towards the center of the circle. This is called Centripetal acceleration. This is also called as Radial acceleration.
Centripetal acceleration, $\left| {{a_c}} \right| = \dfrac{{{v^2}}}{r}$
The force associated with its centripetal acceleration is called centripetal force. It is equal to the mass times the centripetal acceleration.
${F_c} = m{a_c} = \dfrac{{m{v^2}}}{r}$
Consider an airplane moving with its wings inclined at ${30^ \circ }$ to the horizontal.

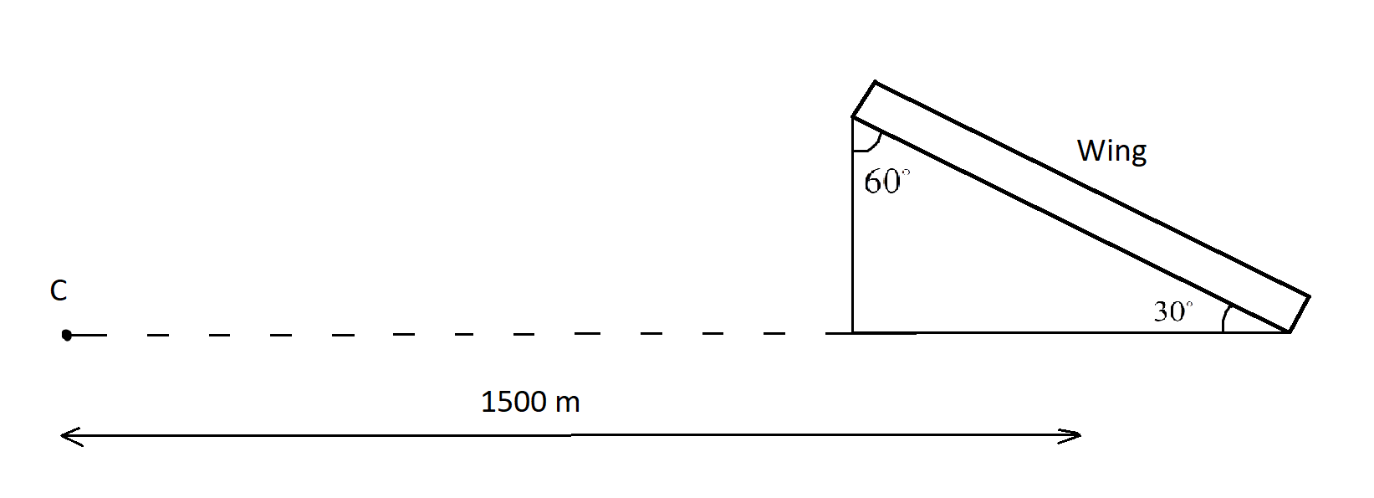
For an airplane to lift off the ground, the lift force should be greater than or equal to the weight of the airplane. This lift force must be equal to the centripetal force so that it remains in the circular path while traveling.
The velocity that the airplane must maintain to be in the circular path is,
${v^2} = rg\tan \theta$
where r is the radius of the turn, g is the acceleration due to gravity and $\theta$ is called as the banking angle.
Given,
Radius of turn, $r = 1500m$
Acceleration due to gravity, $g = 9 \cdot 81m{s^{ - 2}}$
The banking angle represents the inclination of the moving body with respect to the centre. Since, the movement is vertical, the banking angle should be taken as ${60^ \circ }$ as per the figure,
$\theta = {60^ \circ }$
Substituting, we get the velocity
${v^2} = rg\tan \theta$
$\Rightarrow {v^2} = 1500 \times 9 \cdot 81 \times \tan {60^ \circ }$
Solving,
$\Rightarrow {v^2} = 1500 \times 9 \cdot 81 \times \sqrt 3 = 25487 \cdot 12$
$\Rightarrow v = \sqrt {25487 \cdot 12} = 159 \cdot 64 \sim 160m{s^{ - 1}}$

Hence, the correct option is Option C.

Note:
Here, this is an airplane that is moving in the air medium whose centripetal force is balanced by the lift force. Hence, the vertical inclination is considered for the banking angle i.e. ${60^ \circ }$. If it is a vehicle moving on the road, we have to consider the horizontal inclination of the road as the banking angle.